新增3D效果! 群体的智慧!
https://mp.weixin.qq.com/s/LJCdpdiRn9vZe83pf3ysUg
补充一点;3D 效果(双摄像机+mesh)是波波咨询 @杜府 后总结实践;@云谷 是结合上面思路的js代码分享者;白玉无冰是咨询 @波波 和结合@云谷 的代码,再次整理成ts代码,并作图写文整理。 感谢每一位小伙伴的付出

新增3D效果! 群体的智慧!
https://mp.weixin.qq.com/s/LJCdpdiRn9vZe83pf3ysUg
补充一点;3D 效果(双摄像机+mesh)是波波咨询 @杜府 后总结实践;@云谷 是结合上面思路的js代码分享者;白玉无冰是咨询 @波波 和结合@云谷 的代码,再次整理成ts代码,并作图写文整理。 感谢每一位小伙伴的付出
这次就不用物理链条了,换一种方式实现。
在 物理挖洞-优化篇 和 物理挖洞-实现篇 中介绍了一种用多边形链条组件(cc.PhysicsChainCollider)实现物理挖洞的方法。这次打算用多边形碰撞组件(cc.PhysicsPolygonCollider)去实现物理挖洞。
建议先看前两篇的讲解,有助于更快理解这篇文章。
整体思路是,先用 Clipper 去计算多边形,接着用 poly2tri 将多边形分割成多个三角形,最后用多边形刚体填充。
Clipper 是一个强大的用于多边形布尔运算库。前往下面这个地址下载,并作为插件导入 creator 。
http://jsclipper.sourceforge.net
为什么这次不用 物理挖洞-实现篇 中的 PolyBool 呢?
经测试发现 Clipper 的效率会比 PolyBool 高,并且 Clipper 内置了一个方法可以明确知道哪些多边形是洞。
poly2tri 是一个把多边形分割成三角形的库。下载地址如下:
https://github.com/r3mi/poly2tri.js
poly2tri 的使用有一些要注意的,大致就是不能有重复的点,不能有相交的形状。

先在场景中添加一个物理节点,一个绘图组件(用来画图)。
接着把物理引擎打开,监听触摸事件。
// onLoad() {
// 多点触控关闭
cc.macro.ENABLE_MULTI_TOUCH = false;
cc.director.getPhysicsManager().enabled = true;
this.node_dirty.on(cc.Node.EventType.TOUCH_START, this._touchMove, this);
this.node_dirty.on(cc.Node.EventType.TOUCH_MOVE, this._touchMove, this);
// }
为了方便管理多边形碰撞组件,新建一个脚本 PhysicsPolygonColliderEx.ts。
因为物理碰撞体需要物理刚体,我们可以加一些限制,并把这个菜单指向物理碰撞体的菜单中。
const { ccclass, property, menu, requireComponent } = cc._decorator;
@ccclass
@menu("i18n:MAIN_MENU.component.physics/Collider/PolygonEX-lamyoung.com")
@requireComponent(cc.RigidBody)
export default class PhysicsPolygonColliderEx extends cc.Component {
}
我们就可以在刚体节点中添加这个插件脚本了。
既然要用到多边形碰撞体,就定义一个多边形碰撞体数组。
private _physicsPolygonColliders: cc.PhysicsPolygonCollider[] = [];
因为 Clipper 中计算的结构是 {X,Y}。
所以加个变量记录多边形顶点信息。
private _polys: { X: number, Y: number }[][] = [];
因为不同的库用的数据结构不同,所以添加两个转换方法。
private _convertVecArrayToClipperPath(poly: cc.Vec2[]) {
return poly.map((p) => { return { X: p.x, Y: p.y } });
}
private _convertClipperPathToPoly2triPoint(poly: { X: number, Y: number }[]) {
return poly.map((p) => { return new poly2tri.Point(p.X, p.Y) });
}
加一个初始化数据的接口。
init(polys: cc.Vec2[][]) {
this._polys = polys.map((v) => { return this._convertVecArrayToClipperPath(v) });
}
参考 Clipper 中的使用例子,写一个多边形差集调用。
//polyDifference(poly: cc.Vec2[]) {
const cpr = new ClipperLib.Clipper();
const subj_paths = this._polys;
const clip_paths = [this._convertVecArrayToClipperPath(poly)]
cpr.AddPaths(subj_paths, ClipperLib.PolyType.ptSubject, true);
cpr.AddPaths(clip_paths, ClipperLib.PolyType.ptClip, true);
const subject_fillType = ClipperLib.PolyFillType.pftEvenOdd;
const clip_fillType = ClipperLib.PolyFillType.pftEvenOdd;
const solution_polytree = new ClipperLib.PolyTree();
cpr.Execute(ClipperLib.ClipType.ctDifference, solution_polytree, subject_fillType, clip_fillType);
const solution_expolygons = ClipperLib.JS.PolyTreeToExPolygons(solution_polytree);
this._polys = ClipperLib.Clipper.PolyTreeToPaths(solution_polytree);
参考 poly2tri 中的使用,写一个多边形分割成三角形的调用。记得要把上面返回的数据转成 poly2tri 中可以使用的数据格式。
// polyDifference(poly: cc.Vec2[]) {
let _physicsPolygonColliders_count = 0;
for (const expolygon of solution_expolygons) {
const countor = this._convertClipperPathToPoly2triPoint(expolygon.outer);
const swctx = new poly2tri.SweepContext(countor);
const holes = expolygon.holes.map(h => { return this._convertClipperPathToPoly2triPoint(h) });
swctx.addHoles(holes);
swctx.triangulate();
const triangles = swctx.getTriangles();
// 逐一处理三角形...
}
然后再逐一处理分割好的三角形,修改 cc.PhysicsPolygonCollider 的 points 属性。
// 逐一处理三角形...
for (const tri of triangles) {
let c = this._physicsPolygonColliders[_physicsPolygonColliders_count];
if (!c) {
//没有的话就创建
c = this.addComponent(cc.PhysicsPolygonCollider);
c.friction = 0;
c.restitution = 0;
this._physicsPolygonColliders[_physicsPolygonColliders_count] = c;
}
c.points = tri.getPoints().map((v, i) => {
return cc.v2(v.x, v.y)
});
c.apply();
_physicsPolygonColliders_count++;
}
// 剩余不要用的多边形清空。
this._physicsPolygonColliders.slice(_physicsPolygonColliders_count).forEach((v => {
if (v.points.length) {
v.points.length = 0;
v.apply();
}
}));
只要在遍历三角形的时候逐点画线就行了。
if (i === 0) ctx.moveTo(v.x, v.y);
else ctx.lineTo(v.x, v.y);
为了不让每帧计算量过多,添加一个命令队列。
private _commands: { name: string, params: any[] }[] = [];
pushCommand(name: string, params: any[]) {
this._commands.push({ name, params });
}
在每次更新的时候,取出几个命令去执行。
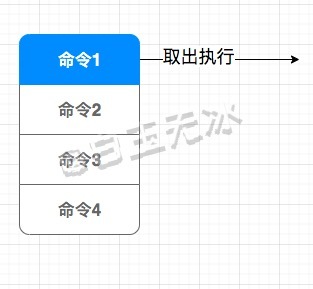
lateUpdate(dt: number) {
if (this._commands.length) {
// 每帧执行命令队列
for (let index = 0; index < 2; index++) {
const cmd = this._commands.shift();
if (cmd)
this[cmd.name](...cmd.params);
else
break;
}
}
}
整体思路和 物理挖洞-优化篇 和 物理挖洞-实现篇 差不多。不清楚的话,可以回看这两篇文章。

这次不同的是,加了一个涂抹步长控制,当涂抹间隔太小的时候,就参与不计算。
private _touchStartPos: cc.Vec2;
private _touchStart(touch: cc.Touch) {
this._touchStartPos = undefined;
this._touchMove(touch);
}
private _touchMove(touch: cc.Touch) {
const regions: cc.Vec2[] = [];
const pos = this.graphics.node.convertToNodeSpaceAR(touch.getLocation());
const count = DIG_FRAGMENT;
if (!this._touchStartPos) {
// 画一个圆(其实是多边形)
for (let index = 0; index < count; index++) {
const r = 2 * Math.PI * index / count;
const x = pos.x + DIG_RADIUS * Math.cos(r);
const y = pos.y + DIG_RADIUS * Math.sin(r);
regions.push(this._optimizePoint([x, y]));
}
this._touchStartPos = pos;
} else {
const delta = pos.sub(this._touchStartPos);
// 手指移动的距离太小的话忽略
if (delta.lengthSqr() > 25) {
// 这里是合并成一个顺滑的图形 详细上一篇文章
const startPos = this._touchStartPos;
for (let index = 0; index < count; index++) {
const r = 2 * Math.PI * index / count;
let vec_x = DIG_RADIUS * Math.cos(r);
let vec_y = DIG_RADIUS * Math.sin(r);
let x, y;
if (delta.dot(cc.v2(vec_x, vec_y)) > 0) {
x = pos.x + vec_x;
y = pos.y + vec_y;
} else {
x = startPos.x + vec_x;
y = startPos.y + vec_y;
}
regions.push(this._optimizePoint([x, y]));
}
this._touchStartPos = pos;
}
}
if (regions.length)
this.polyEx.pushCommand('polyDifference', [regions, this.graphics]);
}
private _touchEnd(touch: cc.Touch) {
this._touchStartPos = undefined;
}
专业挖坑,从未停止。与群内小伙伴讨论后,发现一些坑和可优化的点。。。
之前是使用 cc.graphic 作图的,可能有小伙伴需要填充好看的纹理。
这时,可以巧用 cc.mask 中的 _graphic。
可以清楚的看到, mask 的裁剪实质上是由一个 graphic 作图实现的。
所以我们上面的 graphic 组件可以替换成 mask 中的 _graphic。在该节点添加一个 cc.mask 组件即可。
在代码中获取一下这个这个 graphic,原来的逻辑不变。
this.graphics = this.node_dirty.getComponent(cc.Mask)['_graphics'];
准备一张 256x256 的图片(一定要是2的n次幂),设置为 repeat 模式。并将这个张图片放在 mask 节点下,铺满界面。
看看效果怎么样。
有群友(感谢@两年)反馈,滑动时有概率出现刚体消失。
仔细琢磨后,发现是 poly2tri 这个库有些限制。用 clipper 计算的结果还要加一层处理。
先看第一个报错。
大概是说有自交的多边形。
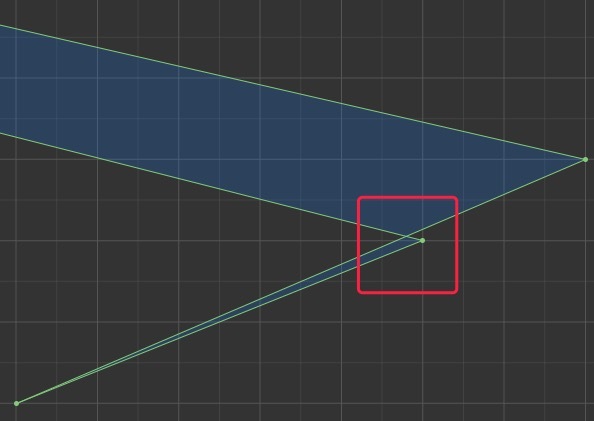
我也没办法呀,这结果是 clipper 算出来的。
还好,clipper 官方文档翻了一阵。找到一个可以用的。
https://sourceforge.net/p/jsclipper/wiki/documentation/
加一个参数,可以实现严格简单的多边形(但是效率更低)。
const cpr = new ClipperLib.Clipper(ClipperLib.Clipper.ioStrictlySimple);
再看另一种情况下的报错。
这个大概是说,出现了共线不支持。
经过我细心分析(日志大法),发现是 clipper 计算的结果中的 holes 和 outer 之间有重复的点时候,就会产生错误。
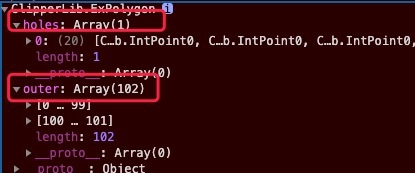
可惜这次没在文档中找到相应的方法处理。

只好自己写一个方法,计算后再过滤一下这些重复的节点。
private _convertClipperPathToPoly2triPoint(poly: { X: number, Y: number }[], exclude: poly2tri.Point[] = []): poly2tri.Point[] {
const newPos: poly2tri.Point[] = [];
poly.forEach((p, i) => {
const p_now = new poly2tri.Point(p.X, p.Y)
const isIn = exclude.some((e_p) => {
if (e_p.equals(p_now)) {
return true;
}
})
if (!isIn) {
newPos.push(p_now);
exclude.push(p_now);
}
})
if (newPos.length > 2)
return newPos;
else
return [];
}
最后,发给热心群(859642112)友,测试后,暂时没出现这个问题了。
加了这些优化,是否会增加了计算量?是否会产生新的卡顿?
每次绘制一个三角形,效率会不会更低?能否直接绘制多边形?减少绘制次数?
如果初始多边形比较大,是否可以分割成几个多边形,分区域划分计算?减少大量多边形计算。
是否可以需要把库拆解?只选取自己需要的部分?根据算法重新设计?这样就不需要转格式了。
…
这些问题,就交给大家去思考了吧!挖洞挖坑,填坑,就像不停歇的球,永不停歇。
以上为白玉无冰使用 Cocos Creator v2.3.3 开发"物理挖洞之多边形碰撞体的实现"的技术分享。如果对你有点帮助,欢迎分享给身边的朋友。
牛啊!!!
减少多边形计算!画饼分之~

在 物理挖洞之链条!实现!(含视频讲解) 中介绍了用 PolyBool 和链条组件(cc.PhysicsChainCollider)实现物理挖洞的方法。
虽说这种方案可能不是最佳方案,但里面有一种 evenodd 的思想,觉得不错的。
在 物理挖洞之链条!优化!(含视频讲解) 中介绍了几个优化的地方。
其中,单位化的思想和平滑移动的思想在后续一直被使用。

不过,多边形链条组件有一个问题,容易穿透。
接着,经过多次查找和分析,在物理挖洞之多边形!实现! 中介绍用多边形碰撞组件(cc.PhysicsPolygonCollider)去实现物理挖洞。
整体思路是,先用 Clipper 去计算多边形 (效率比 PolyBool 高),接着用 poly2tri 将多边形分割成多个三角形,最后用多边形刚体填充。
但是呢,poly2tri 限制比较多,物理挖洞之多边形!填坑! 中介绍了填坑之路。
并利用 mask 的 graphics 实现好看的纹理。
当然,还有群内小伙伴们讨论分享的3D效果,在上面的基础上,修改了一个物理挖洞之3D效果,感谢各位小伙伴的分享!
强烈建议按顺序阅读上面几篇文章,有助于更好的理解这篇的文章哦!
整体思路是对区域进行分块,点击的时候判断是对哪个区域块有操作,再对这些区域块进行多边形计算,最后再绘制所有的多边形。

这里与物理挖洞之多边形!实现! 中的区别是少了一步 poly2tri,这是怎么做到的?
首先得明白一点,之前使用 poly2tri 是因为会有内多边形出现。
所以,在分块的时候,只要满足分块的尺寸小于挖洞的尺寸,这样就不会出现内多边形了。

如何判断点击的是哪个区域呢?
在初始化的时候,用一个2D矩形(cc.Rect)数组记录每一个分块的信息。
private _rects: cc.Rect[] = [];

当点击的时候会生成一个多边形(参考物理挖洞之链条!优化! 中的触摸平滑连续)数据。
对于这个多边形的每个点,计算出坐标 x 和 y 的最大值和最小值。
然后就可以算出这个的多边形的矩形(aabb (Axis-Aligned Bounding Box))。
let xMin = Number.MAX_SAFE_INTEGER, xMax = Number.MIN_SAFE_INTEGER, yMin = Number.MAX_SAFE_INTEGER, yMax = Number.MIN_SAFE_INTEGER;
// 计算最小最大值
xMin = p.x < xMin ? p.x : xMin;
yMin = p.y < yMin ? p.y : yMin;
xMax = p.x > xMax ? p.x : xMax;
yMax = p.y > yMax ? p.y : yMax;
// 得出矩形
const rect_r = cc.Rect.fromMinMax(cc.v2(xMin, yMin), cc.v2(xMax, yMax));

再用这个矩形和初始化矩形做一次相交判断,这样就可以粗略的确定要计算的块了。
for (let index = 0; index < this._rects.length; index++) {
const rect = this._rects[index];
if (rect.intersects(rect_r)) {
this.polyEx.pushCommand('polyDifference', [regions, index])
}
}

多边形计算用的是 Clipper ,使用接口可以参考官网或者物理挖洞之多边形!。
// polyDifference(poly: cc.Vec2[], index: number) {
// 计算新的多边形
// https://sourceforge.net/p/jsclipper/wiki/documentation
const cpr = new ClipperLib.Clipper(ClipperLib.Clipper.ioStrictlySimple);
const subj_paths = this._polys[index];
const clip_paths = [this._convertVecArrayToClipperPath(poly)]
cpr.AddPaths(subj_paths, ClipperLib.PolyType.ptSubject, true);
cpr.AddPaths(clip_paths, ClipperLib.PolyType.ptClip, true);
const subject_fillType = ClipperLib.PolyFillType.pftEvenOdd;
const clip_fillType = ClipperLib.PolyFillType.pftEvenOdd;
const solution = new ClipperLib.Paths();
cpr.Execute(ClipperLib.ClipType.ctDifference, solution, subject_fillType, clip_fillType);
this._polys[index] = solution || [];
在所有分块计算之后,最后整体绘制多边形碰撞体和纹理。
// private draw() {
ctx.clear();
for (let index = 0; index < this._polys.length; index++) {
const polygons = this._polys[index];
for (let index2 = 0; index2 < polygons.length; index2++) {
const polygon = polygons[index2];
let c = this._physicsPolygonColliders[_physicsPolygonColliders_count];
c.points = this._convertClipperPathToVecArray(polygon);
c.apply();
for (let index3 = 0; index3 < c.points.length; index3++) {
const p = c.points[index3];
if (index3 === 0) ctx.moveTo(p.x, p.y);
else ctx.lineTo(p.x, p.y);
}
ctx.close();
}
}
ctx.fill();
当然,群(859642112)内小伙伴 @吴先生 也实现了这个分块,分块计算多边形同时,也进行分块绘制,欢迎加群一起讨论!
生命不息,挖坑不止!
以上为白玉无冰使用 Cocos Creator v2.3.3 开发"物理挖洞之分块!"的技术分享。如果对你有点帮助,欢迎分享给身边的朋友。
天下事有难易乎?为之,则难者亦易矣;不为,则易者亦难矣。人之为学有难易乎?学之,则难者亦易矣;不学,则易者亦难矣。 --《为学》

mark…
战术插个眼
太厉害了呀!
插眼
mark。
mark mark
膜拜大佬!
mark 挖洞功能 感谢分享
插个眼。。
markdown
MARK插入
请问下 只能是矩形吗?如果是弹弹堂那种地形,你这个方法适用吗?
厉害厉害 
mark!
mark,五个字符