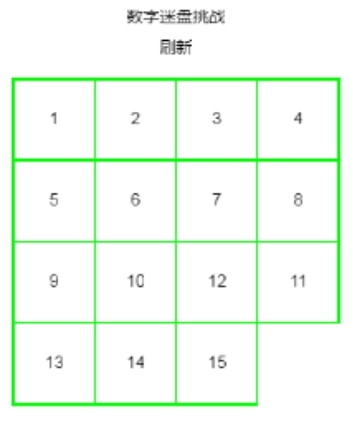
这种情况是不是无解,什么原因导致,有什么方法可以避免无解情况的出现,望各路大神赐教
这个问题我读研的时候恰好研究过.我自创了个方法你试试.
你把所有临界的两个值的差 都加起来. 只有偶数或者奇数, 要么是奇数不可解要么是偶数我忘了, 仅仅把14和15反过来的一种情况都是不可解的.
具体的我忘了. 反正就是研究一下求相邻的差.
是不是说,临界的两个值的差都加起来的值是奇数或者偶数(其中某一个)的情况,是无解的,对吧
兄嘚,不知道我是否理解错误,我试了一下,不靠谱啊
之前写的,别人博客总结的规律,有解的情况。忘了是啥了。你参考一下
getRandomTable: function (c,r) {
var seedList = new Array(r*c);
for (var i = 0; i < seedList.length; i++) {
seedList[i] = i;
}
var tempList = new Array();
for (var i = 0; i < c; i++) {
tempList[i] = new Array();
for (var j = 0; j < r ; j++) {
var rIndex = this.RandomInt(0,seedList.length);
tempList[i][j] = seedList[rIndex];
seedList[rIndex] = seedList[seedList.length - 1];
seedList.pop();//删除最后一个
}
}
return tempList;
},
IsAvailable: function (data) {
//数据不符合规格
if(data == null || data.length <=1 || data[0].length <= 1 ){
return false;
}
var cN = data.length;
var rN = data[0].length;
var tranceTb = new Array(rN*cN);
var pc = 0;
var pr = 0;
for (var r = 0; r < rN; r++) {
for (var c = 0; c < cN; c++) {
if (data[c][r] == cN*rN-1) {
pc = c;
pr = r;
}
tranceTb[r*cN +c] = data[c][r];
}
}
var sumT = 0;
for (var i = 0; i < tranceTb.length; i++) {
if (cN*rN -1 == tranceTb[i]) {
continue;
}
var counter = 0;
for (var j = i+1; j < tranceTb.length; j++) {
if (tranceTb[i] > tranceTb[j]) {
counter ++;
}
}
sumT = sumT + counter;
}
if (cN%2 != 0 && sumT%2 == 0 ) {
return true;
}
if (cN%2 == 0) {
if ((rN-pr)%2 != 0 && sumT%2 == 0 ) {
return true;
}
if ((rN-pr)%2 == 0 && sumT%2 != 0 ) {
return true;
}
}
return false;
},
getAvailableTable: function (c,r) {
var maxCounter = 100;//最多次数
var result = new Array©;
while(maxCounter >= 0){
result = this.getRandomTable(c,r);
if(this.IsAvailable(result) == true){
return result;
}
maxCounter --;
}
return -1;
},
具体的细节我忘了. 因为我做的功能是4x4任意情况的自动求解.当时证明了所有情况的刚好一半不可解.
计算前最后一格填个偶数,比如16,而且必须只能空这一格.
最终情况为偶数60. 则当你计算任意棋盘值为奇数则无解.
但是还研究了一个更浅显易懂的方法:
初始情况的每一个格子上的数字直接与最终的应该放到的格子位置上的数字交换,16个格子你最多做15次就能交换成最终的结果. 然而你会发现用不到15次就交换好了.然而.这个次数,只要是偶数就有解,只要是奇数就无解.
当然初始情况必须只能空最后一格.
举例:
|1 2 3 4|
|5 6 7 8|
|9 11 12 15|
|13 10 14 x|
---- 第1次 交换
|1 2 3 4|
|5 6 7 8|
|9 10 12 15|
|13 11 14 x|
---- 第2次 交换
|1 2 3 4|
|5 6 7 8|
|9 10 11 15|
|13 12 14 x|
---- 第3次 交换
|1 2 3 4|
|5 6 7 8|
|9 10 11 12|
|13 15 14 x|
---- 第4次 交换
|1 2 3 4|
|5 6 7 8|
|9 10 11 12|
|13 14 15 x|
—>总共用了4次,4是偶数 所以有解(其实就是把右下角轮转了一下组成的)
例2:
|1 2 3 4|
|5 6 7 8|
|9 10 11 12|
|13 15 14 x|
—> 第1次交换
|1 2 3 4|
|5 6 7 8|
|9 10 11 12|
|13 14 15 x|
–> 总共用了1次,1为奇数,所以无解
例3:
|2 3 4 8|
|1 6 7 15|
|5 11 12 14|
|9 13 10 x|
–1:
|1 3 4 8|
|2 6 7 15|
|5 11 12 14|
|9 13 10 x|
–2:
|1 2 4 8|
|3 6 7 15|
|5 11 12 14|
|9 13 10 x|
–3:
|1 2 3 8|
|4 6 7 15|
|5 11 12 14|
|9 13 10 x|
–4:
|1 2 3 4|
|8 6 7 15|
|5 11 12 14|
|9 13 10 x|
–5:
|1 2 3 4|
|5 6 7 15|
|8 11 12 14|
|9 13 10 x|
–6:
|1 2 3 4|
|5 6 7 8|
|15 11 12 14|
|9 13 10 x|
–7:
|1 2 3 4|
|5 6 7 8|
|9 11 12 14|
|15 13 10 x|
–8:
|1 2 3 4|
|5 6 7 8|
|9 10 12 14|
|15 13 11 x|
–9:
|1 2 3 4|
|5 6 7 8|
|9 10 11 14|
|15 13 12 x|
–10:
|1 2 3 4|
|5 6 7 8|
|9 10 11 13|
|15 14 12 x|
–11:
|1 2 3 4|
|5 6 7 8|
|9 10 11 12|
|15 14 13 x|
–12:
|1 2 3 4|
|5 6 7 8|
|9 10 11 12|
|13 14 15 x|
– 12为偶数,所以有解,实际上是例1的基础上空位又转了一圈得到的
** 另外只要能转成例2 的那种形式,那一定无解
同理: 你截图的那种情况 11 12交换1次就为结果, 1为奇数因此无解
更简单的说就是写个选择排序,真正的交换次数和为奇数则无解,和为偶数则有解,简单吧?
哈哈哈,厉害,很好,我去研究研究,不懂问问您
我去试试,谢谢了
