-
Creator 版本: 2.4.0
-
目标平台: windows
Cocos Creator 坐标+向量+数学Math [个人理解+记录]
- 1.坐标
-
1.1 可以参考官方大大新写的文档::坐标系和节点变换属性
-
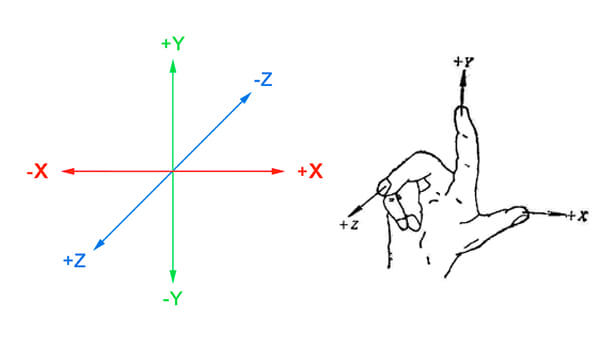
1.2 Cocos Creator 笛卡尔右手坐标系例图::
-
1.3 常用坐标转换(具体的可以研究内部数据)::
let getTempNode=this.node;
// 获取节点世界坐标(比较常用这个::::::)(计算的坐标固定一些,方便向量计算)
let worldPosition = getTempNode.convertToWorldSpaceAR(cc.v2(0, 0));
// 转换坐标点到节点下(计算相对坐标可以)
let position = getTempNode.convertToNodeSpaceAR(cc.v2(0,0));
1.4+++ 待添加内容…
2.向量(向着某个方向移动,用尺子测量长度,点状方向坐标)
-
2.0 向量::位移(带有方向,大小的有向线段)
-
2.0.1 向量就是可以理解为,A点到B点之间的一条线段,是一个有方向的线段,就叫向量
-
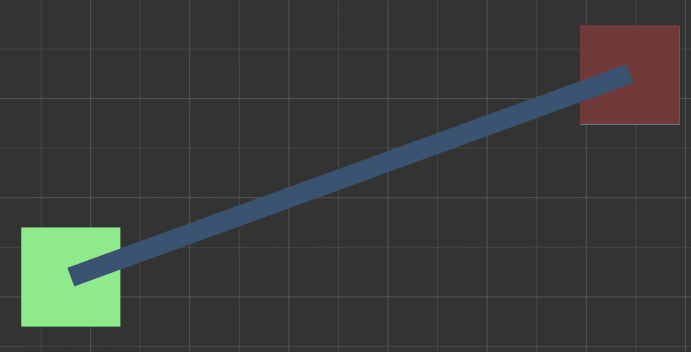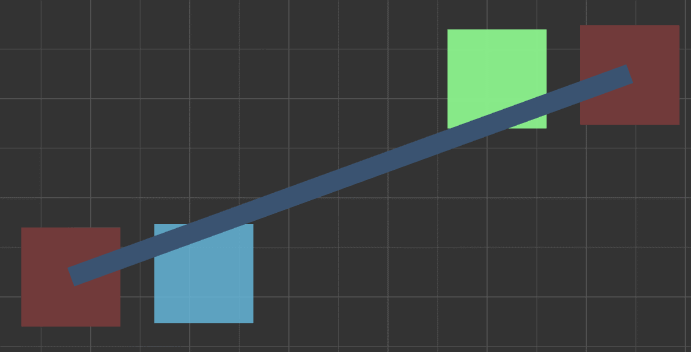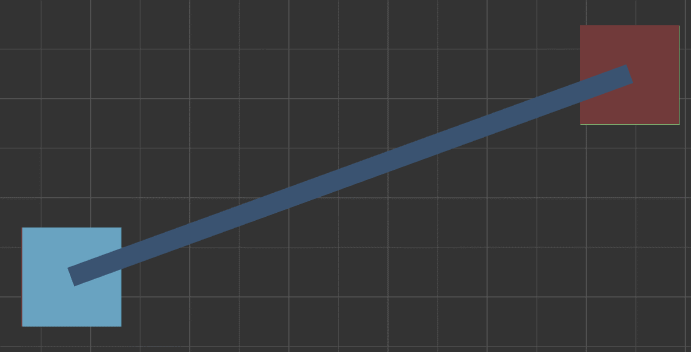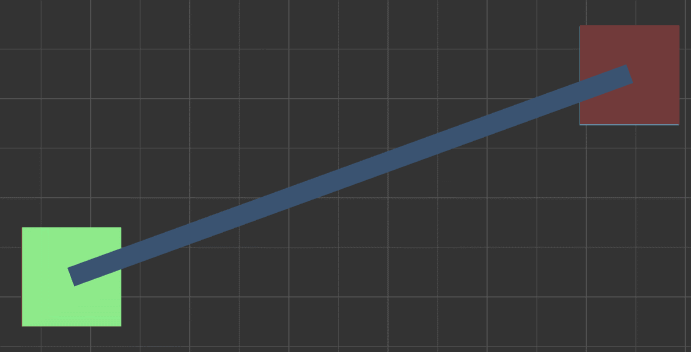
2.0.2 简单示意图,向量C::
-
2.1 向量归一化,计算向量长度,向量缩放(其实就是把一个有方向的向量化成了数字1)
-
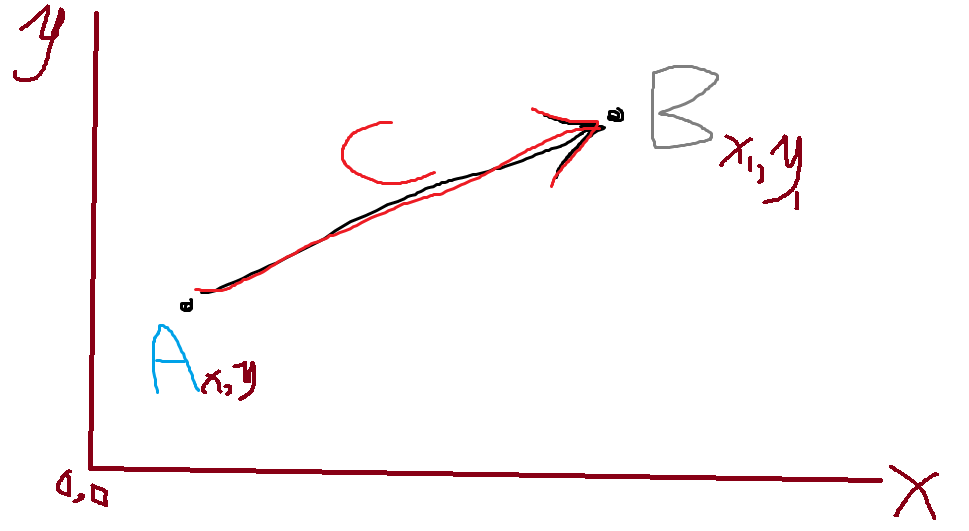
2.1.0 引用上面的截图,点A,点B,
let pointA=cc.v2(0,0);
let pointB=cc.v2(300,400);
// 向量长度计算1::
// let lengC= 直角三角形计算方式= 两条边的平方和开根号
let lengA=300,lengB=400;
// 简单三边三角数, 300*300+400*400=500*500
let lengC1=Math.sqrt(lengA*lengA+lengB*lengB,2);
// cocos向量长度计算2::
let lengC2=pointA.sub(pointB).mag();
// 向量缩放mul,求向量C的中点的坐标::
// 数学书上也有,不过cocos简单点,直角坐标系,向量缩放0.5
// mul_pos1=cc.v2(150,200);
let mul_pos1=pointB.mul(0.5)||pointB.sub(pointA).mul(0.5)
||pointB.multiplyScalar(0.5)||pointB.mulSelf(0.5);
// 缩放当前向量。如果你想结果保存到另一个向量,可使用 mul() 代替。
// mulSelf(num: number): Vec2;
// 缩放向量,并返回新结果。
// mul(num: number, out?: Vec2): Vec2;
// 缩放当前向量
// multiplyScalar(num: number): Vec2;
// 原理介绍::=>
// 缩放当前向量 mulSelf(num: number): Vec2;
// cc.v2(3,4).mulSelft(0.5); => cc.v2(1.5,2);
// x=3*0.5;
// y=4*0.5;
// 坐标x,y乘以0.5
//向量除法 divSelf(num: number): Vec2;
// cc.v2(3,4).divSelf(0.5); => cc.v2(6,8);
// x=3/0.5;
// y=4/0.5;
// 坐标x,y除以0.5
// lerp 线性插值移动::
// from: number, to: number, ratio: number
// a=初始值,b=目标值, radio变化速率
// lerp(a: number, b: number, r: number): number;
// cc.misc.lerp(2,10,0.5)//returns 6
// this.camera.node.position.lerp(this.targetPos, dt * 2.0, this.targetPos);
// this.sceneMainCamera.zoomRatio = cc.misc.lerp(this.sceneMainCamera.zoomRatio, 0.5, 3.14 * dt);
// node.worldPosition = node.worldPosition.lerp(_target, speed * dt);
// 原理介绍::=>
// 逐元素线性插值: A + t * (B - A)
function lerp(a,b,t){
return a+(b-a)*t;
};
// 向量归一化,sub两个向量相减,求出正确要归一的向量,然后归一化
// getNormLeng的值就是1::
let getNormLeng=pointA.sub(pointB).normalizeSelf().mag();
// 向量归一化以后,就变成了500个1的集合::
let getNormPos=pointA.sub(pointB).normalizeSelf();
// 可以如此应用,用来移动Node节点,Move::
// 由A点移动到B点,C向量的1/3点,中点
let Move_pos1=pointB.sub(pointA).normalizeSelf().mul(pointA.sub(pointB).mag()/3);
let Move_pos1=pointB.sub(pointA).normalizeSelf().mul(pointA.sub(pointB).mag()/2);
// 由A点移动到B点,终点
let Move_pos1=pointB.sub(pointA).normalizeSelf().mul(pointA.sub(pointB).mag());
2.2 开发者工具的,console控制台输出调试::
2.3+++ 待添加内容…
3.数学
3.1 三角函数
-
3.1.1 正弦(待添加示例代码)
数学术语,在直角三角形中,任意一[锐角]∠A的[对边]与[斜边]的比叫做∠A的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边
古代说法,正弦是股与[弦]的比例
现代[正弦公式]是
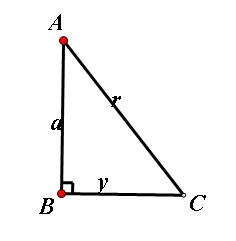
sin = 直角三角形的对边比斜边.
如图,斜边为r,对边为y,邻边为a。斜边r与邻边a夹角Ar的正弦sinA=y/r
无论a,y,r为何值,正弦值恒大于等于0小于等于1,即0≤sin≤1.
-
3.1.2 余弦(待添加示例代码)
余弦(余弦函数),三角函数的一种。在Rt△ABC(直角三角形)中,∠C=90°(如概述图所示),∠A的余弦是它的邻边比三角形的斜边,即cosA=b/c,也可写为cosa=AC/AB。余弦函数:f(x)=cosx(x∈R)

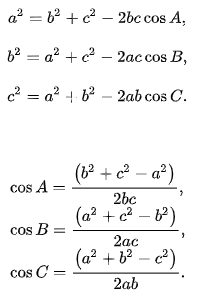
-
3.1.3 弧度角度转换
// 三角函数,内30°角对边的顶点坐标,带方向的夹角的弧度signAngle,
let a=-cc.v2(Math.sqrt(27),3).normalize().signAngle(cc.v2(1, 0))*(180/Math.PI);
// 角度转弧度
angle_to_radian (angle: number): number {
// 角度转弧度公式
// π / 180 * 角度
// 计算出弧度
let radian = Math.PI / 180 * angle;
// 返回弧度
return(radian);
}
// 弧度转角度
radian_to_angle (radian: number): number {
// 弧度转角度公式
// 180 / π * 弧度
// 计算出角度
let angle = 180 / Math.PI * radian;
// 返回弧度
return(angle);
}
// 角度转向量
angle_to_vector (angle: number): Vec2 {
// tan = sin / cos
// 将传入的角度转为弧度
let radian = this.angle_to_radian(angle);
// 算出cos,sin和tan
let cos = Math.cos(radian);// 邻边 / 斜边
let sin = Math.sin(radian);// 对边 / 斜边
let tan = sin / cos;// 对边 / 邻边
// 结合在一起并归一化
let vec = new Vec2(cos, sin).normalize();
// 返回向量
return(vec);
}
// 向量转角度
vector_to_angle (vector: Vec2): number {
// 将传入的向量归一化
let dir = vector.normalize();
// 计算出目标角度的弧度
let radian = dir.signAngle(new Vec2(1, 0));
// 把弧度计算成角度
let angle = -this.radian_to_angle(radian);
// 返回角度
return(angle);
}
- 3.1.4 三角函数验算+演算
Math.ceil((Math.atan2(Math.floor(Math.sqrt(27)),3)*180)/Math.PI)==60
// true
Math.floor((Math.atan2(3,Math.round(Math.sqrt(27)))*180)/Math.PI)==30
// true
Math.sin(30*((Math.PI)/180))==Math.sin(30*((2*Math.PI)/360))
// true
Math.sin(45) * 2
// 1.7018070490682369
Math.sin(45)
// 0.8509035245341184
(180/Math.PI*0.8509035245341184)
// 48.75318072861148
Math.sin(45*Math.PI/180)
// 0.7071067811865475
(180/Math.PI*0.7071067811865475)
// 40.51423422706977
Math.sin(45*(Math.PI/180))
// 0.7071067811865475
45*(Math.PI/180)
// 0.7853981633974483
(180/Math.PI*0.7853981633974483)
// 45
// 碰撞互斥转角度移动
node.position = this.get_random_pos();
const collide = node.getComponent(LQCollide);
collide.on_collide = () => {
node.color = cc.Color.GREEN;
node.x += Math.cos(node.radians) * 10;
node.y += Math.sin(node.radians) * 10;
- 3.1.5 圆周运动,参考 金币落袋
/**
* 以某点为圆心,生成圆周上等分点的坐标
*
* @param {number} r 半径
* @param {cc.Vec2} pos 圆心坐标
* @param {number} count 等分点数量
* @param {number} [randomScope=80] 等分点的随机波动范围
* @returns {cc.Vec2[]} 返回等分点坐标
*/
getCirclePoints(r: number, pos: cc.Vec2, count: number, randomScope: number = 60): cc.Vec2[] {
let points = [];
let radians = (Math.PI / 180) * Math.round(360 / count);
for (let i = 0; i < count; i++) {
let x = pos.x + r * Math.sin(radians * i);
let y = pos.y + r * Math.cos(radians * i);
points.unshift(cc.v3(x + Math.random() * randomScope, y + Math.random() * randomScope, 0));
}
return points;
}
3.2 矩阵转换(先写个大概的,具体的还不太明白,各位大大有懂的也可以评论一下,感谢)
- 矩阵转换,详细可参考帖子 【乐府】使用2种方式实现动画的动态蒙版
// 场景中两个并列的节点 A 和 B
let M_a = cc.mat4(); // A 的世界矩阵
getTempNodeA.getWorldMatrix(M_a);
let M_a_invert = cc.mat4(); // A 世界矩阵的逆矩阵
M_a.invert(M_a_invert);
let M_b = cc.mat4(); // B 的世界矩阵
getTempNodeB.getWorldMatrix(M_b);
let M_a2b = cc.mat4(); // A 到 B的变换矩阵
M_b.mul(M_a_invert, M_a2b);
3.3 +++ 后续添加的内容(杂)…
// 三角函数关键角度计算阈值:::
(Math.atan2(3,Math.sqrt(27))*(180/Math.PI))!=(-cc.v2(Math.sqrt(27),3,0).normalize().signAngle(cc.v3(1, 0,0))*(180/Math.PI))&&
Math.floor(Math.atan2(3,Math.sqrt(27))*(180/Math.PI))==Math.floor(-cc.v2(Math.sqrt(27),3,0).normalize().signAngle(cc.v3(1, 0,0))*(180/Math.PI))
// 自定义二进制buffer文件内容:::
var thebuff2 = new ArrayBuffer(136);
var tetbuff2 = new Int8Array(thebuff2);
var forArr2 = [-122, 0, 64, 68, 100, 0, 9, 0, 6, 0, 0, 0, 0, 0, 0, 0, 6, 0, 0, 0, 0, 0, 0, 0, -6, -1, -1, -1, -1, -1, -1, -1, -6, -1, -1, -1, -1, -1, -1, -1, 6, 0, 0, 0, 0, 0, 0, 0, 6, 0, 0, 0, 0, 0, 0, 0, -6, -1, -1, -1, -1, -1, -1, -1, -6, -1, -1, -1, -1, -1, -1, -1, 2, 0, 0, 0, 0, 7, 13, 12, 59, 11, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 4, 2, 0, 0];
for (var kA2 = 0; kA2 < forArr2.length; kA2++) {
tetbuff2[kA2] = forArr2[kA2];
};
var tetbufdataview2 = new DataView(thebuff2);
let bse_Set = cc.director.getScene().getComponentInChildren("cc.Canvas").getComponent("testBuffer")||cc.director.getScene().children[0].getComponent("testBuffer");
b_Set.m_pSetLayer.node.active = true;
b_Set.on_gend(tetbufdataview2, 126);
dUb_stringToUint8Array(str: any): Uint8Array {
var arr = [];
for (var i = 0, j = str.length; i < j; ++i) {
arr.push(str.charCodeAt(i));
}
var tmpUint8Array = new Uint8Array(arr);
return tmpUint8Array;
};
dUb_Uint8ArrayToString(fileData: any): string {
var dataString = "";
for (var i = 0; i < fileData.length; i++) {
dataString += String.fromCharCode(fileData[i]);
};
return dataString;
};
// 多边形相交绘制:::=>
polygonRedDrawLine(t: any, allPointArr: any, e: any, col: any) {
this.redGraphics.lineWidth = 13.14/5;
this.redGraphics.strokeColor = col || cc.Color.RED;
let getPointArr = allPointArr || this._redPoints || [];
// 画个小圆圈::
if (this.startDraw) {
this.redGraphics.circle(t.x, t.y, 14.5);
this.redGraphics.stroke();
};
// lineJoin: Graphics.LineJoin;
// !#zh 线段拐角属性 * /
// export enum LineJoin {
// BEVEL = 0,
// ROUND = 0,
// MITER = 0,
// }
// !#zh 线段末端属性 */
// export enum LineCap {
// BUTT = 0,
// ROUND = 0,
// SQUARE = 0,
// }
// lineCap: Graphics.LineCap;
// ellipse(cx ?: number, cy ?: number, rx ?: number, ry ?: number): void;
// roundRect(x ?: number, y ?: number, w ?: number, h ?: number, r ?: number): void;
if (getPointArr.length >= 2) {
var e = getPointArr[getPointArr.length - 2];
// cc.log("getPointArr.length==", [getPointArr.length]);
// 线段设置起始点::
// this.redGraphics.lineJoin = 1;
// this.redGraphics.LineCap = 1;
// 来个椭圆和圆角矩形::
// 渐变椭圆形::
// this.redGraphics.ellipse(e.x, e.y, e.x / 5, e.y / 2);
// 步增椭圆::
// this.redGraphics.ellipse(e.x, e.y, 55 / 5, 33 / 2);
// 圆角矩形::
// this.redGraphics.roundRect(e.x, e.y, 95, 38, 3);
// 向量归一化防止断点绘图!::
this.redGraphics.lineWidth = 13.14;
this.redGraphics.moveTo(t.x, t.y);
// 同心圆:::多圈::
// let getValNormal = t||e.sub(t);
// getValNormal = e||e.sub(t);
// getValNormal = e.sub(t);
let getSubVec2=e||e.sub(t);
let getMagLen=getSubVec2.mag();
let getValNormal = getSubVec2.normalizeSelf();
// getValNormal.mul(getMagLen);
// 分型成12份吧,不要太满::
let getTempNum = 11, tempMulNum2 = 0.01, tempVec2 = null;
// cc.log("getValNormal==",[getValNormal.x,getValNormal.y]);
for (var ii = 0; ii < getMagLen; ii+=100) {
tempVec2 = getValNormal.mul(ii);
// 用圆形,填充空隙::
// cc.log("tempVec2.x, tempVec2.y=",[tempVec2.x, tempVec2.y])
// if(tempVec2.x<5){debugger;}
// if (getPointArr.length > 3) {
this.redGraphics.circle(tempVec2.x, tempVec2.y, 3.14/2);
// };
};
this.redGraphics.lineTo(e.x, e.y);
this.redGraphics.stroke();
};
};
// 射线碰撞检测::=>
let postName=null,postRayCast=cc.director.getPhysicsManager().rayCast(cc.v2(0,0),cc.v2(tempNode.getPosition().x,tempNode.getPosition().y), cc.RayCastType.AllClosest);
postRayCast.length>0?(postName=postRayCast[0].collider.name):(postName=null);
let allRayCastPhyCollider = [];
if (postRayCast.length > 0) {
for (let i = 0; i < postRayCast.length; i++) {
allRayCastPhyCollider.push(postRayCast[i].collider.name);
};
console.log("射线碰到的节点是::==", [allRayCastPhyCollider, postRayCast]);
};
// 加入个最小最大值判断原型:::
if (typeof Array.prototype['max'] == 'undefined') {
// Array.max = function (array) {
// return Math.max.apply(Math, array);
// };
// Array.min = function (array) {
// return Math.min.apply(Math, array);
// };
//最小值
Array.prototype.min = function () {
var min = this[0];
var len = this.length;
for (var i = 1; i < len; i++) {
if (this[i] < min) {
min = this[i];
}
}
return min;
}
//最大值
Array.prototype.max = function () {
var max = this[0];
var len = this.length;
for (var i = 1; i < len; i++) {
if (this[i] > max) {
max = this[i];
}
}
return max;
}
};
// 循环写入目前距离:::
for (let ii = 0; ii < this.allPlayers.length; ii++) {
this.allLengMag[ii] = this.guaiWuAIplayer.node.position.sub(this.allPlayers[ii].node.position).mag();
};
// 取出最小距离玩家的index:::
this.zuiJinPlayerIndex = this.allLengMag.indexOf(this.allLengMag.min());


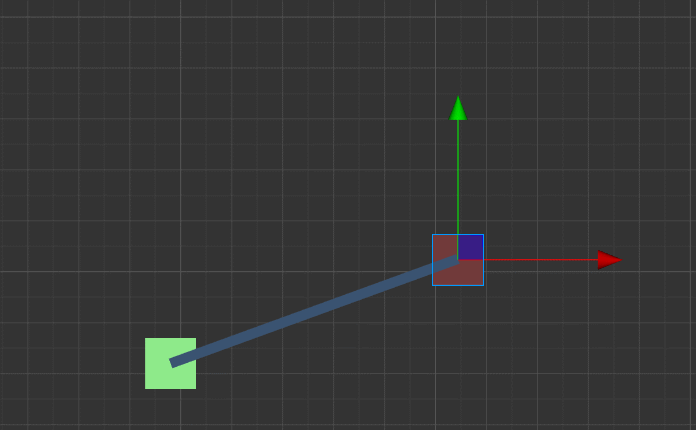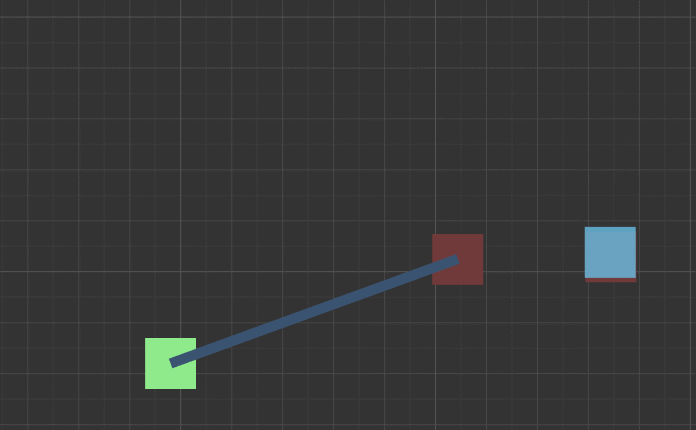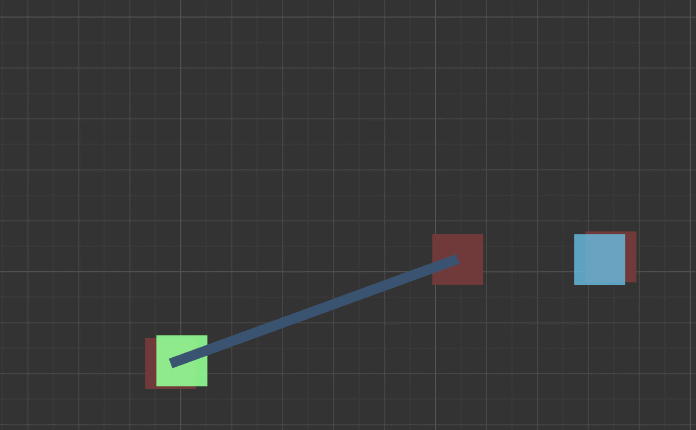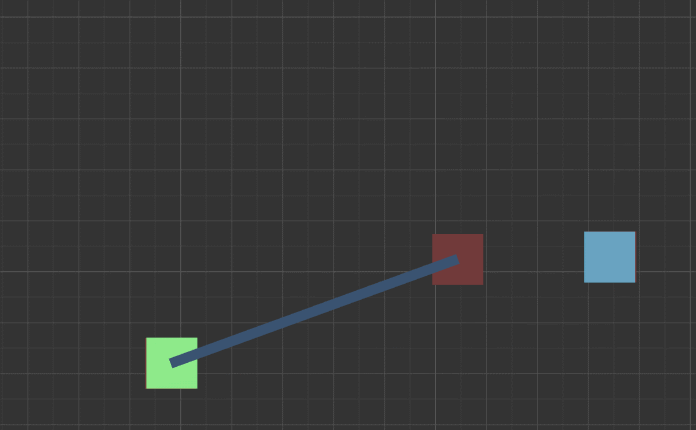



 听说现在小学就开始教三角函数了
听说现在小学就开始教三角函数了