围绕矩形中心点旋转后如何得到新的四个顶点坐标

Creator 2.x
#1

已知矩形中心点(x1,y1) 宽(w) 宽(h) 角度(angle_ > 0) 求四个点坐标
let rectwidth = w / 2;
let rectheight = h / 2;
let xx1 = -Math.cos(angle_) * rectwidth - Math.sin(angle_) * rectheight + x1;
let yy1 = -Math.sin(angle_) * rectwidth + Math.cos(angle_) * rectheight + y1;
let xx2 = -Math.cos(angle_) * rectwidth + Math.sin(angle_) * rectheight + x1;
let yy2 = -Math.sin(angle_) * rectwidth - Math.cos(angle_) * rectheight + y1;
let xx3 = Math.cos(angle_) * rectwidth + Math.sin(angle_) * rectheight + x1;
let yy3 = Math.sin(angle_) * rectwidth - Math.cos(angle_) * rectheight + y1;
let xx4 = Math.cos(angle_) * rectwidth - Math.sin(angle_) * rectheight + x1;
let yy4 = Math.sin(angle_) * rectwidth + Math.cos(angle_) * rectheight + y1;
这是我写的得到 左上(xx1,yy1) 左下(xx2,yy2) 右下(xx3,yy3) 右上(xx4,yy4)

#2

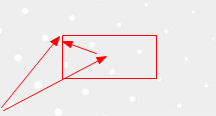image 矢量旋转

#3

容我理解下矢量旋转是啥

#4

等你搞cocos 3d的四元数旋转会怀疑人生

#5

现在已搞得我 晕头转向 感觉我写得对 一运行就是不对

#6

我记得cocos有现成的api计算向量旋转的

#7

求知啊 有现成当然用现成得 自己算头好大

#8

https://github.com/cocos/cocos-engine/blob/v3.7.2/cocos/core/math/vec2.ts#L794

#9

是我网络问题吗？打不开

#10

网络问题 打开了

#11

transformMat4 是这个api吗？

#12

我给你发的链接带了行号啊，你点进去的那一行就是啊

#13

看见了 谢谢

#14

你 算法只能在一向限内用 用矢量就没有这个问题…

#15

xcosA - ysinA + p.x = x1，xsinA + ycosA + p.y = y1，其实就是把矩形顶点乘以旋转矩阵，在移动到p点（围绕旋转的点）

#16

感谢大家恢复 容我试试都