体验地址:
ClothDemo|2.x版本:提供几个应用示例(幕布,绳子?)
ClothDemo|3.7.3版本:有3D场景
起源
前两天刷知乎,看到了一个好玩的效果

效果地址:可撕裂网格
正巧是以前见过的一个效果,最近又刷到了,以前觉得好难,也看不懂,现如今再回头看,又是另一番感悟。
于是研究代码,准备移植到Cocos一下,也算是还愿吧。
分析与拓展
整个效果可以拆成两部分,一部分是网格的模拟,一部分是网格的渲染。
-
模拟这块,暂且按人家的算法,照搬也没什么难度,注意兼容就好。
-
渲染就更简单了,直接使用Graphic组件,画线就好。
嗯,还原度很高。
似乎这就完事了,但是还没有!
在研究代码的时候,发现是基于质点弹簧系统,将整个网格划分为一个个质点,并通过模拟弹簧,来决定质点之间的位置关系。
再结合渲染那块的知识,质点与渲染顶点数据其实非常接近,如果我能将这个质点传入之间直接渲染的话,那我就得到一个2D的真实的布料?同理,像软体,果冻,弯曲的绳子,头发 这种,都可以通过这个方式去实现!
突然感觉自己以前想做但不会的一些效果与功能,现在都有迹可循。
一切都只依赖于,自定义顶点数据,也不需要定义顶点格式,甚至cocos就有支持,sprite的mesh。
于是就有了下面的拓展内容。
2D的布料
在整体搬运代码之后,加上自定义顶点数据,就得到了一个最基础的2D布料效果,嗯,很舒服,比单纯的网格舒服多了,而且也有一定的实用性了。
但是问题也来了,网格划分越多,整个布料就被拉伸的越扭曲,受重力影响也越大。
多算法的实现
于是,在对代码的研究加上网上资料的整理,我找到了质点弹簧系统与PBD算法。
大多数实现都是Unity的,但是原理是相同的,在搬运与调试中,也学到了不少内容。
参考了几种写法后,最后发现,要达到一个好的效果,不仅需要选择一个适合的算法,同样需要对不同场景,调试一些参数,比如 迭代次数,步进时长,还有更细一点的 弹簧密度之类的,根据实现不同,参数也不一样。
这几种算法本身就是3D的,2D其实本身就是简化内容。
而且整个布料系统,不仅仅是对软体布料这种东西的模拟,而且可以与其他物体产生碰撞(模拟),甚至还能对物体产生反作用力。
其实这个在游戏中应用非常广泛,譬如,3D游戏中,人物 飘荡的裙子,头发,旗帜之类的,这种 需要有物理效果,但不参与碰撞或碰撞对象很少的内容,也解答了我之前对这块的疑惑。
看过大佬的最牛逼的案例是,一个3D的布料,能与3D物体互相作用,就像一块真实的布料。
但是搬运之后,自己测试,达不到这个效果,一方面是js可能性能跟不上,有些参数调不上去,而且Unity有JobSystem配合Burst编译,性能非常给力啊,另一方面也是自己太菜吧。
大家可以自己去试着实现这个功能,还有很有意思的,收获良多,也可以看看我实现的几个例子
体验地址:
ClothDemo|2.x版本:提供几个应用示例(幕布,绳子?)
ClothDemo|3.7.3版本:有3D场景
商店链接:
以下是学习过程中,整理的一些内容。
质点弹簧系统
质点弹簧系统(Mass-spring system)是一种物理动力学模型,用于描述由固定点和质点以及它们之间的弹簧构成的物理系统。
质点弹簧系统通常用于模拟柔软的物体、布料、绳索、发丝等物体的运动行为。
该模型可以通过欧拉法、隐式欧拉法、Leapfrog 等数值方法进行求解,并可以与碰撞检测、重力、摩擦力等效应相结合,以更准确地模拟复杂的物理场景。
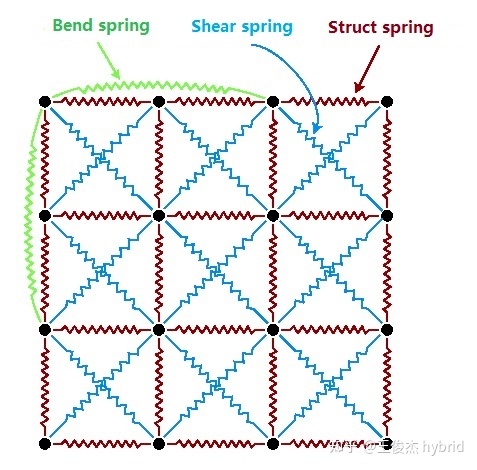
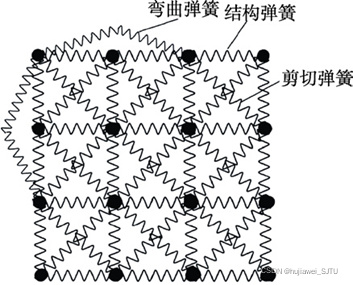
结构化的弹簧网格,它的简化形式如下:
在弹簧网格中,存在着三种弹簧:
-
结构弹簧(Struct spring),用于提供弹簧拉伸和压缩的力
-
剪切弹簧(Shear spring),用于在弹簧发生剪切变形时提供剪切力
-
弯曲弹簧(Bend spring),用于避免弹簧发生过度翻折
通过这个结构,我们就可以模拟出一个布料效果。
布料模拟中的显示积分、隐式积分和PBD
在布料模拟中,可以使用不同的方法来进行计算和模拟,其中比较常见的有显示积分、隐式积分和基于位置的动力学(PBD)算法。下面是它们各自的特点和优劣性:
显式积分
最直观朴素的方式去更新顶点:
- 根据弹簧两端的顶点位置和弹簧原长,计算每根弹簧的力
- 求与顶点连接的所有弹簧,所产生的合力,用以更新每个顶点的速度和位置
这就是我们最容易想到的,也最容易理解的方法。
显式积分方法将受力计算和速度更新分离开来,先根据当前状态计算出力,然后根据力和时间步长计算出速度和位移。这种方法通常比较简单,易于实现,但需要保证时间步长足够小,否则可能会导致数值不稳定。
由于采样是离散的,k太大或采样频率不够(步长太大)时,弹簧很可能会出现左右晃荡,最终越跑越远的系统崩溃问题。
每次都更偏离原长,所以每次获得的力都更大,恶性循环,最终整张布会被扯得稀烂。
-
优点:
-
实现简单
-
计算速度较快
-
-
缺点:
-
时间步长需要足够小才能保证数值稳定
-
容易出现震荡等问题
-
隐式积分
所谓隐式,与显式最大的不同在于,它用下一时刻的力来更新当前的速度和位置,这就是一个先有鸡还是先有蛋的问题了。
隐式积分方法将受力计算和速度更新同时进行,通过求解一个方程组来得到下一时刻的节点位置。这种方法可以保证数值稳定,但通常计算量较大,需要使用迭代方法来求解方程组。
-
优点:
-
数值稳定
-
可以处理较大的时间步长
-
-
缺点:
-
计算复杂度高
-
运行速度慢
-
现实世界的织物一旦拉伸超过一定限度,就会强烈抵抗拉伸限制。
但是,增加刚度会导致问题。
显式积分器将不稳定。解决方案:更小的时间步长和更多的计算时间。
隐式积分器中涉及的线性系统将是病态的。解决方案:更多的迭代和计算时间。
PBD算法
PBD 算法使用基于位置的动力学模型,通过约束来调整节点的位置,从而达到模拟布料的效果。它不需要像积分方法那样使用速度和加速度等物理参数,只需要处理节点位置与约束条件之间的关系。
-
优点:
-
可在 GPU 上并行 (PhysX)
-
简单易于实现
-
可以在大时间步长下保持稳定
-
可以处理多种约束,包括流体
-
-
缺点:
-
不是基于物理的。弹性系数受到网格点,迭代次数的影响。
-
高分辨率下性能低下
-
精度有限
-
需要进行迭代求解
-
综合来看,显式积分方法简单易用,但需要控制时间步长以保证数值稳定;隐式积分方法可以保证数值稳定,但计算复杂度较高;PBD 算法则是一种基于约束的模拟方法,可以在大时间步长下保持稳定,并且具有较好的扩展性,但精度相对较低。因此,在实际应用中需要根据具体需求选择合适的方法。
参考文章
参考文章1
ChatGPT