引言
最近在看《显微镜下的大明之丝绢案》,剧中帅家默的父亲教给帅家默一种快速丈田的方法,叫推步聚顶之术。
剧中口诀如下
先牵经纬以衡量,再点原初标步长。田型取顶分别数,再算推步知地方。
我对此颇为感兴趣,经过研究和查证资料,剧中的推步聚顶之术其实就是鞋带公式(Shoelace Formula),
也称为高斯面积公式。是由Albrecht Ludwig Friedrich Meister (1724-1788)在1769年,
基于高斯(Carl Friedrich Gauss)和C.G.J. Jacobi. 的梯形公式提出的。
此公式可以简单快速地得出平面上任意多边形的面积。
因为利用多边形坐标进行交叉相乘,像是系鞋带,所以称之为鞋带公式。
这个公式在游戏开发中还是非常有用的,所以今天我就来教大家利用这个公式来实现任意多边形的面积计算。
涉及知识
- TypeScript
- CocosCreator3.x
- 代数几何
鞋带公式详解
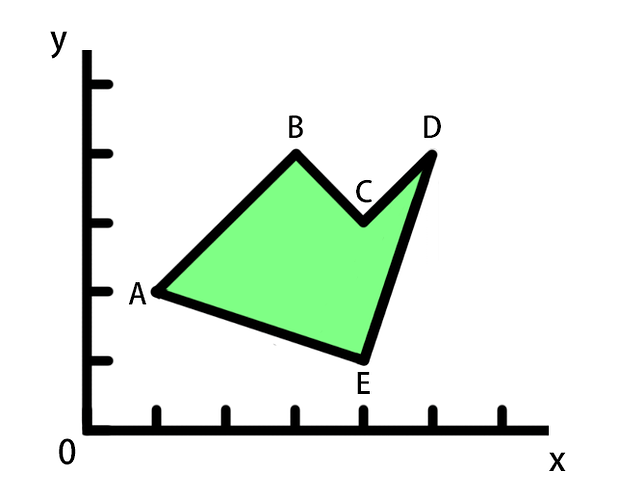
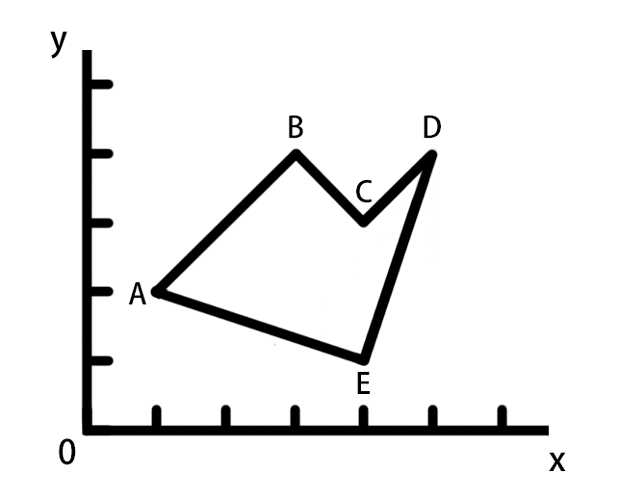
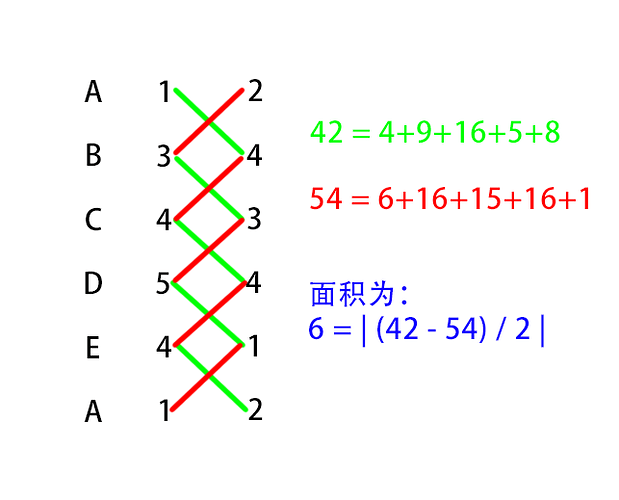
如图所示,我们有一个多边形,我们要计算它的面积。他有五个顶点,分别如下
- A(1,2)
- B(3,4)
- C(4,3)
- D(5,4)
- E(4,1)
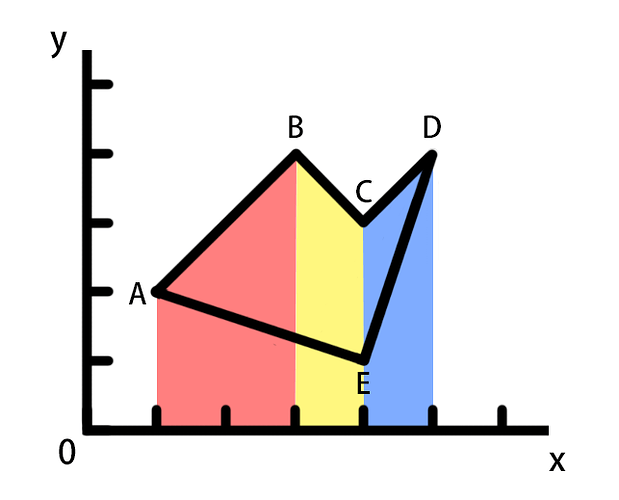
从A点遍历到D点,可以分别计算出下图红色,黄色,蓝色梯形面积,计算公式为(y1+y2) * (x2-x1) / 2,此时梯形的高为正数
相加后得到下图绿色部分面积
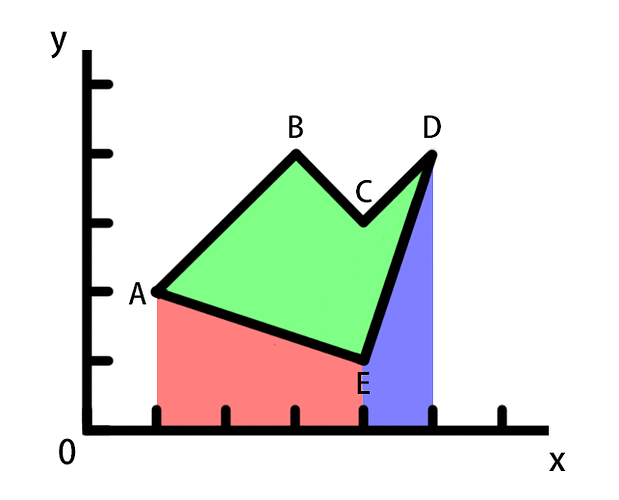
继续从D点遍历回到A点,由于此时x方向为负,所以在公式中梯形的高为负数,那么就会从上图绿色部分面积中减去下图红色和紫色部分面积
最后得出该多边形面积为 6
完整计算公式为
(ya+yb) * (xb-xa) / 2 + (yb+yc) * (xc-xb) / 2 + (yc+yd) * (xd-xc) / 2 + (yd+ye) * (xe-xd) / 2 + (ye+ya * (xa-xe) / 2
整理后得如下图所示
应用场景
-
玩家领地计算:开放世界游戏中,玩家圈地后实时计算所围区域面积决定资源产量。
-
物理碰撞精准化: 复杂多边形碰撞体自动面积计算,用于模拟真实物理效果(如碎片大小影响重力)。
核心代码
先写一段js代码进行测试,
输入项为多边形的顶点坐标数组,输出项为多边形的面积。
/**
* 鞋带公式
* @param {x: number, y: number}[] points 多边形的顶点坐标数组
* @returns {number} 多边形的面积
*/
function calculateArea(points) {
if (points.length < 3) return 0;
let sum = 0;
let p1;
let p2;
const loopTimes = points.length - 1;
for (let i = 0; i < loopTimes; i++) {
p1 = points[i];
p2 = points[i + 1];
sum += (p2.x - p1.x) * (p1.y + p2.y);
}
p1 = points[0];
p2 = points[loopTimes];
sum += (p1.x - p2.x) * (p2.y + p1.y);
return Math.abs(-sum * 0.5);
}
/**
* 三角形
* 0
* /\
* 1--2
*/
const triangle = [
{x: 0, y: 0},
{x: 10, y: 0},
{x: 10, y: 10},
];
console.log(calculateArea(triangle)); // 50
/**
* 四边形
* 0-----1
* | |
* 3-----2
*/
const quad = [
{x: 0, y: 0},
{x: 10, y: 0},
{x: 10, y: 10},
{x: 0, y: 10},
];
console.log(calculateArea(quad)); // 100
/**
* 多边形,上面的例子
*/
const polygon = [
{x: 1, y: 2},
{x: 3, y: 4},
{x: 4, y: 3},
{x: 5, y: 4},
{x: 4, y: 1},
];
console.log(calculateArea(polygon)); // 6

如上Demo我们已经正确计算了输入三角形和四边形的面积。
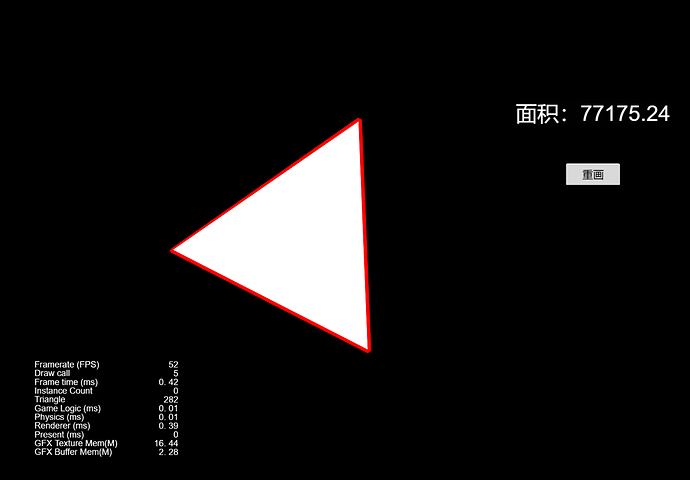
在Cocos中实现简单demo画出多边形并计算面积
剧中的推步聚顶之术跨次元实锤!我们只需点击鼠标,1秒就能算出古人辛苦半日的丈田结果。
搭建一个场景,添加三样东西
-
Graphics组件用于绘制 - 一个按钮用于清空
- 一个文本框用于显示面积
新建脚本CalcArea.ts并挂载到Canvas节点上
核心代码如下
import {_decorator, Button, Component, EventTouch, Graphics, input, Input, Label, Node, UITransform, v2, v3, Vec2} from 'cc';
const {ccclass, property} = _decorator;
@ccclass('CalcArea')
export class CalcArea extends Component {
@property(Graphics) graphics: Graphics = null;
@property(Node) clearBtn: Node = null;
@property(Label) txt: Label = null;
// 前绘制点
private points: Vec2[] = [];
start() {
input.on(Input.EventType.TOUCH_START, this.onTouchStart, this);
input.on(Input.EventType.TOUCH_END, this.onTouchEnd, this);
this.clearBtn.on(Button.EventType.CLICK, this.clickClear, this);
}
clickClear() {
this.graphics.clear();
this.points = [];
}
onTouchStart(event: EventTouch) {
const pos = event.getUILocation();
const localPos = this.getComponent(UITransform)
.convertToNodeSpaceAR(v3(pos.x, pos.y, 0));
this.graphics.clear();
this.points.push(v2(localPos.x, localPos.y));
}
onTouchEnd(event: EventTouch) {
const pos = event.getUILocation();
const localPos = this.getComponent(UITransform)
.convertToNodeSpaceAR(v3(pos.x, pos.y, 0));
// 添加新顶点并重绘和计算
this.points.push(v2(localPos.x, localPos.y));
this.drawFinalPolygon();
const area = this.calculateArea(this.points);
this.txt.string = `面积:${area.toFixed(2)}`;
}
// 绘制多边形
private drawFinalPolygon() {
this.graphics.clear();
this.graphics.moveTo(this.points[0].x, this.points[0].y);
for (const p of this.points) {
this.graphics.lineTo(p.x, p.y);
}
this.graphics.close();
this.graphics.fill();
this.graphics.stroke();
}
// 计算多边形面积,鞋带公式
private calculateArea(points: Vec2[]): number {
if (points.length < 3) return 0;
let sum = 0;
let p1: Vec2;
let p2: Vec2;
const loopTimes = points.length - 1;
for (let i = 0; i < loopTimes; i++) {
p1 = points[i];
p2 = points[i + 1];
sum += (p2.x - p1.x) * (p1.y + p2.y);
}
p1 = points[0];
p2 = points[loopTimes];
sum += (p1.x - p2.x) * (p2.y + p1.y);
return Math.abs(-sum * 0.5);
}
}
如图所示,对于简单三角形和任意多边形,我们都可以计算出面积。
注意事项
- 多边形的顶点坐标必须按照顺时针或者逆时针顺序排列
结语
鞋带公式在游戏开发中还是非常有用的,以上就是我对鞋带公式的简单介绍,没有包含数据的校验等相关内容,不过希望对你有所帮助。