点击上方码不了一点+关注和★ 星标
统治游戏几何运算,碾压海伦公式丨数学江湖的刀光剑影
引言
在游戏开发的广阔天地中,几何计算无处不在。从精确的碰撞检测到高效的路径规划,从逼真的地形生成到炫酷的粒子效果,几何运算都扮演着核心角色。而作为几何图形基石的三角形,其面积计算更是众多复杂运算的基础。
海伦公式(Heron’s formula)作为计算三角形面积的经典方法,虽有着悠久历史和广泛应用,但在实际开发中却暗藏隐忧。浮点数误差的累积可能导致计算结果偏离,而多次开方运算也带来不小的性能开销。在追求精确和高效的游戏开发领域,这些缺陷常常成为无法忽视的瓶颈。
本文将为你揭秘一种更为优雅、高效的三角形面积计算方法——向量积法。这种方法不仅计算过程简洁直观,而且数值稳定性出色,已在众多主流游戏引擎和图形库中得到广泛应用。通过深入对比两种方法的实现原理和性能表现,我们将领略数学之美如何转化为高效代码的精彩过程。
本文以以往文章代码库
涉及知识
- TypeScript
- CocosCreator3.x
- 计算几何学
海伦公式
- 海伦公式是用来计算三角形面积的公式。
- 海伦公式的表达式是:
- S = √[p(p-a)(p-b)(p-c)]
- p = (a+b+c)/2
- a,b,c 是三角形的三条边。
- S 是三角形的面积。
- p 是周长的一半。
由于本文不是具体介绍海伦公式,所以这里不做推导
本文重点不在推导海伦公式,因此略过具体证明过程。
海伦公式的代码实现
function calcTriangleByHeron(p1, p2, p3) {
// 计算三条边长度
const a = Math.sqrt(Math.pow(p2.x - p1.x, 2) + Math.pow(p2.y - p1.y, 2));
const b = Math.sqrt(Math.pow(p3.x - p2.x, 2) + Math.pow(p3.y - p2.y, 2));
const c = Math.sqrt(Math.pow(p1.x - p3.x, 2) + Math.pow(p1.y - p3.y, 2));
// 计算半周长
const s = (a + b + c) / 2;
// 计算面积
return Math.sqrt(s * (s - a) * (s - b) * (s - c));
}
const triangle = [
{x: 0, y: 0},
{x: 10, y: 0},
{x: 10, y: 10},
];
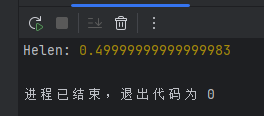
console.log("Heron:", calcTriangleByHeron(...triangle)); // 50
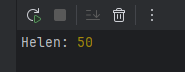
从输出结果可以看到,我们成功计算出该三角形的面积为 50 平方单位。
海伦公式的局限性
尽管海伦公式在数学上很优雅,但在实际编程中却存在明显缺陷:
- 浮点数误差累积导致计算结果不够准确
- 多次开方运算带来较高的计算成本
比如下面这个例子,我们计算另一个三角形的面积
const triangle2 = [
{x: 0, y: 0},
{x: 1, y: 0},
{x: 1, y: 1},
];
console.log("Heron:", calcTriangleByHeron(...triangle2)); // 0.5
向量积法:更优雅的解决方案
向量积法是通过向量叉乘计算三角形面积的方法,其核心步骤非常简洁:
- 选择一个顶点作为参考点
- 计算该顶点与其他两个顶点的向量
- 对这两个向量进行叉乘
- 取叉乘结果的绝对值除以2
向量积法的数学原理
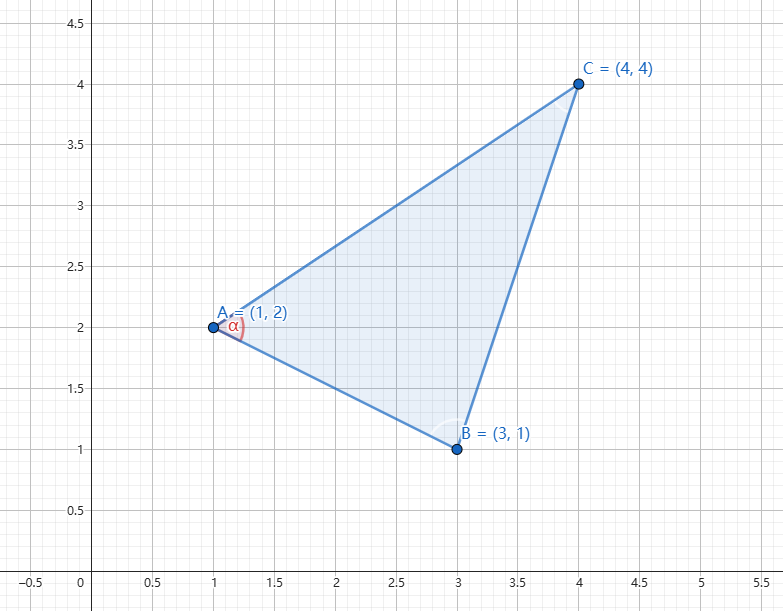
众所周知,计算三角形面积的经典公式是"底乘高除以2"。然而在游戏开发中,我们通常只能直接获取顶点坐标,而非底和高。
如果你幼儿园课上没有打瞌睡,你肯定知道下面这个三角形面积公式
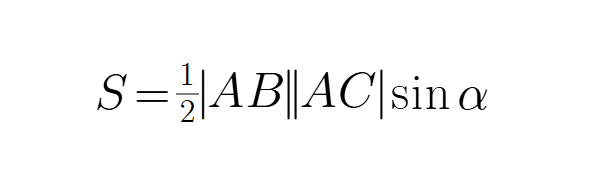
其中:
- |AB| 表示向量AB的长度
- |AC| 表示向量AC的长度
- sin(α) 是向量AB与AC之间夹角的正弦值
为什么使用sin(α)?
这是因为,当我们从B点向AC做垂线时,垂线长度恰好等于sin(α) × |AB|。此时,|AC|作为三角形的底边,垂线长度则为高,完美对应了"底乘高除以2"的公式。
那么得出结论这个公式其实就是众所周知的底乘高除以2
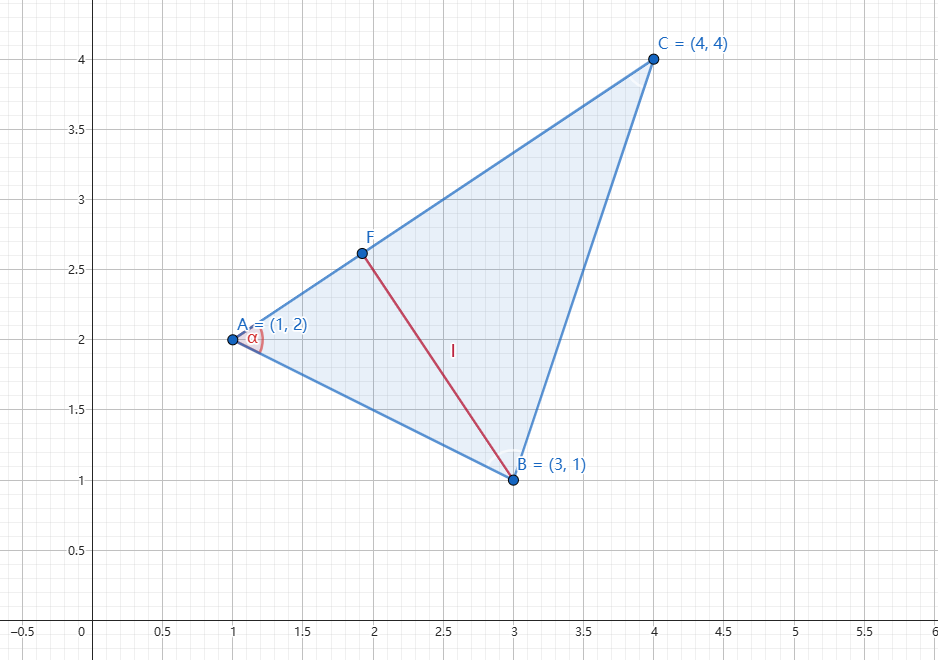
如果你小学线性代数课认真听讲,一定能发现上面这个公式的后边部分和叉乘非常像
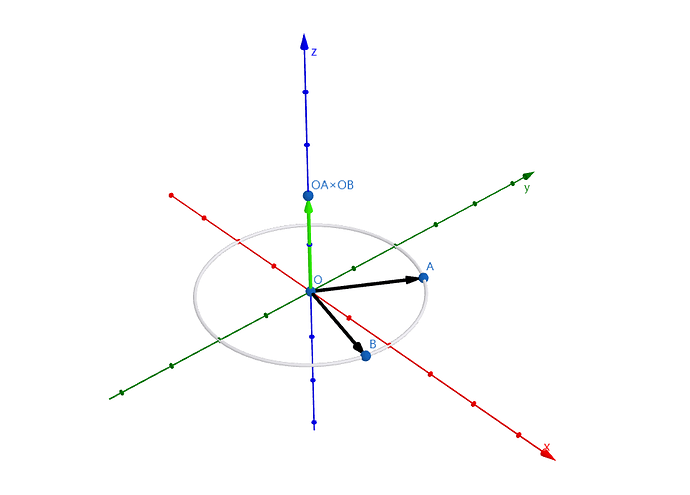
在三维空间中,向量叉乘的结果是一个新向量,其模长正好等于:
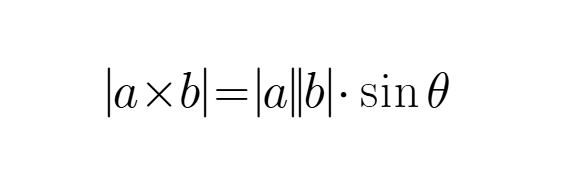
破案!
向量积法的代码实现
// 向量叉乘
const cross = (p1, p2) => p1.x * p2.y - p1.y * p2.x;
function calcTriangleByVector(p1, p2, p3) {
const v1 = { x: p2.x - p1.x, y: p2.y - p1.y }; // 向量p1p2
const v2 = { x: p3.x - p1.x, y: p3.y - p1.y }; // 向量p1p3
return Math.abs(cross(v1, v2)) / 2;
}
const triangle = [
{x: 0, y: 0},
{x: 10, y: 0},
{x: 10, y: 10},
];
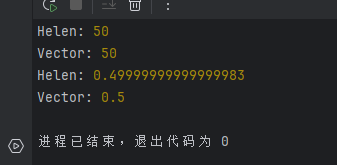
console.log("Vector:", calcTriangleByVector(...triangle)); // 50
const triangle2 = [
{x: 0, y: 0},
{x: 1, y: 0},
{x: 1, y: 1},
];
console.log("Vector:", calcTriangleByVector(...triangle2)); // 0.5
运行结果显示,向量积法不仅计算正确,而且相比海伦公式,明显减少了浮点数误差的累积。
实时对比演示
在Cocos Creator中,我们编写了一个互动Demo,直观展示两种方法的计算差异:
从演示中可以明显看出,海伦公式在特定情况下会产生浮点数误差,而向量积法则保持了稳定的计算精度。
完整代码已上传至仓库,感兴趣的读者可自行下载体验:
本文以以往文章代码库
结语
三角形面积计算虽是几何运算中最基础的问题,却在游戏和图形开发中有着不可替代的地位。通过本文对比,我们看到了海伦公式虽然在数学上很优雅,但在实际应用中可能因浮点数误差和计算效率问题而不够理想。相比之下,向量积法不仅计算逻辑更为简洁,而且数值稳定性更好,已成为众多游戏引擎的首选方案。
这种向量方法的价值远不止于此,它还可以优雅地扩展到计算任意多边形面积、判断点是否在多边形内部等更复杂的几何问题。在性能至上的游戏开发领域,这类算法优化能带来显著的效率提升。
数学之美不仅在于公式的优雅表达,更在于如何将抽象原理转化为高效的代码实现。希望本文能为你的游戏开发之旅增添一把锋利的几何运算利器。
欢迎在评论区分享你在游戏开发中遇到的几何计算难题,让我们一起探索更多优雅高效的解决方案!
点击上方码不了一点+关注和★ 星标