Cocos 3.8版本下Vec3.slerp计算出来的结果会产生Infinity或者NaN

Creator 3.x
#1

用Vect3.lerp是没有问题的

  • Creator 版本：3.8.0

  • 目标平台：编辑器预览

  • 重现方式：必现

  • 首个报错： 无调用堆栈，就是计算结果有误

  • 编辑器操作系统：windows10

  • 重现概率： 必现

截图和代码如下
if (dist > this.followDistance) {

        Vec3.subtract(this._offsetPos, this.targetNode.worldPosition, this.node.worldPosition);

        this._offsetPos.multiply3f((dist / this.followDistance) - 1, (dist / this.followDistance) - 1, (dist / this.followDistance) - 1);

        Vec3.add(this._offsetPos, this.node.worldPosition, this._offsetPos);

        console.log('+++++++++++++++');

        console.log(this._offsetPos);

        console.log('===================');

        console.log(this.node.worldPosition);

        console.log('--------------');

        Vec3.slerp(this._offsetPos, this.node.worldPosition, this._offsetPos, deltaTime > 1 ? 1 : deltaTime);

        console.log(this._offsetPos);

        console.log('AAAAAAAAAAAAAAAAAAA='+deltaTime);

        this.node.setWorldPosition(this._offsetPos);

    }

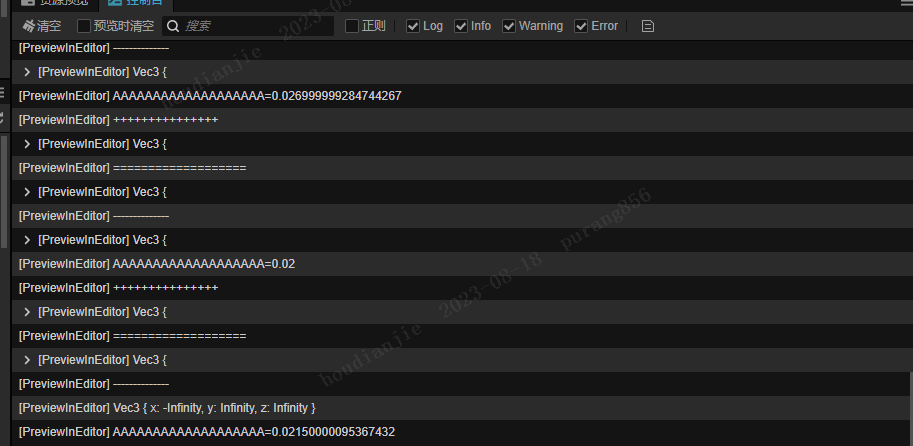
微信截图_20230818190247
微信截图_20230818190247913×446 19.3 KB

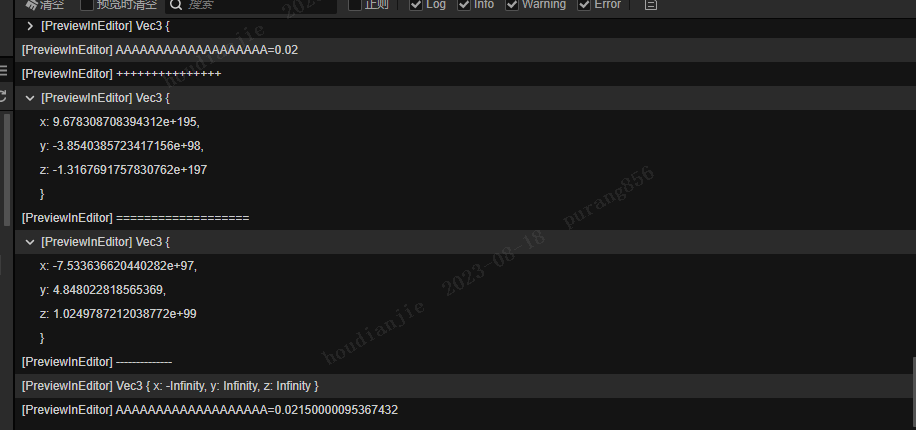
微信截图_20230818190306
微信截图_20230818190306916×430 17.4 KB

#2

能否直接给下 slerp 各个参数的值？你截图里面的打印出来的各个输入参数已经是错误的值了，所以没法复现。

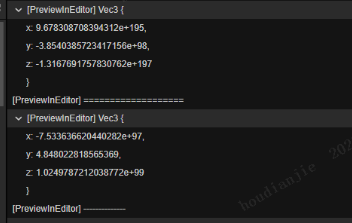
image

这几个输入是超大的数/超小的数。

#3

控制台输出的就是这些值，是slerp函数在lateUpdate里面不停计算得出的，用这些值计算后就会得出NaN，必现的

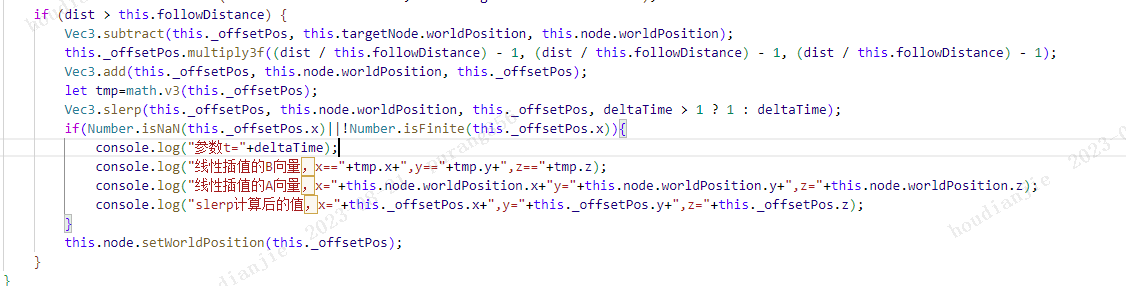
微信截图_20230821105242
微信截图_202308211052421126×286 28.7 KB
微信图片_20230821105256
微信图片_202308211052562400×1080 286 KB

#4

image
image1291×216 73.8 KB

这几个输入都很大，这正常吗？

#5

你比如说这个 B 向量，它的长度是无穷大的：

image

#6

我刚才想用两个初始向量调用该方法复现这个问题，发现不能复现，但是我在自己的程序中实际使用每次都会必现这个问题，程序代码是没办法提供给你们，目前我的解决方式就只能使用lerp函数代替，
上面的那些无穷数值也是计算出来的

#7

([A向量：x=32,y=5,z=-20][B向量：x=-12.05391274983743,y=-8.553789623637115,z=174.03775223657198][参数t:4.513500000238419][结果向量：x=-12.05391274983743,y=-8.553789623637115,z=174.03775223657198])
([A向量：x=-12.05391274983743,y=4.997222185134888,z=174.03775223657198][B向量：x=618.1074623824767,y=-50.11410198145256,z=-2601.5407838733154][参数t:3.46][结果向量：x=618.1074623824767,y=-50.11410198145256,z=-2601.5407838733154])
([A向量：x=618.1074623824767,y=4.991671442985535,z=-2601.5407838733154][B向量：x=-199238.90708315774,y=-1001.239130137733,z=877679.0694758866][参数t:0.02399999976158142][结果向量：x=-4178.460839060863,y=-19.15786755504759,z=18525.193652485672])
([A向量：x=-4178.460839060863,y=4.9833526611328125,z=18525.193652485672][B向量：x=9954189.36176612,y=-7106.934381201556,z=-43843623.57309272][参数t:0.085][结果向量：x=842282.8040823797,y=-599.5296547171957,z=-3709757.4515208574])
([A向量：x=842282.8040823797,y=4.972270727157593,z=-3709757.4515208574][B向量：x=-400513377736.1969,y=-1426563.864344913,z=1764081993302.5283][参数t:0.08300000071525573][结果向量：x=-33241838265.24309,y=-118400.24218873252,z=146415404858.29922])
([A向量：x=-33241838265.24309,y=4.9584304094314575,z=146415404858.29922][B向量：x=623872717391565700000,y=-56303088172.287506,z=-2.7478798161708916e+21][参数t:0.0825][结果向量：x=51469499154304780000,y=-4645004769.664359,z=-226700084699762430000])
([A向量：x=51469499154304780000,y=4.941836595535278,z=-226700084699762430000][B向量：x=-1.495635667107915e+39,y=-87176037751447030000,z=6.587605047347576e+39][参数t:0.08349999904632568][结果向量：x=-1.2488557677716157e+38,y=-7279199069108278000,z=5.500650151710929e+38])
([A向量：x=-1.2488557677716157e+38,y=4.922494173049927,z=5.500650151710929e+38][B向量：x=8.805428540368381e+75,y=-2.1152391094962714e+38,z=-3.878396776185185e+76][参数t:0.08350000023841857][结果向量：x=7.352532852201375e+74,y=-1.7662246614725095e+37,z=-3.238461317361447e+75])
([A向量：x=7.352532852201375e+74,y=4.900407791137695,z=-3.238461317361447e+75][B向量：x=-3.0521078536526385e+149,y=-1.245329160034488e+75,z=1.3443167707179707e+150][参数t:0.08300000071525573][结果向量：x=-2.5332495403620665e+148,y=-1.0336232117359132e+74,z=1.1157829293112185e+149])
([A向量：x=-2.5332495403620665e+148,y=4.875582456588745,z=1.1157829293112185e+149][B向量：x=3.6231129566146925e+296,y=-4.290670420210782e+148,z=-1.5958189367239276e+297][参数t:0.08299999952316284][结果向量：x=3.0071837367138456e+295,y=-3.561256428315438e+147,z=-1.3245297098714022e+296])
([A向量：x=3.0071837367138456e+295,y=4.848022818565369,z=-1.3245297098714022e+296][B向量：x=-Infinity,y=-Infinity,z=Infinity][参数t:0.08399999976158143][结果向量：x=-Infinity,y=-Infinity,z=Infinity])

#8

从数据来看，下一帧的A向量就是上一帧的结果向量？那么 B 向量的值是根据什么计算的？我确实看到 B 向量在不断的变大，那么结果是会一直变大的。

#9

B向量的计算过程：
1、获取目标节点和相机节点之间的位置向量差，赋值给B向量
2、B向量×距离比例。距离比例：（当前两节点实际距离/允许停止跟随的最大距离）-1
3、将相机节点位置向量与B向量相加的结果赋值给B向量
4、执行Vec3.slerp函数：Vec3.slerp(B向量，相机节点位置向量，B向量，时间t)
5、计算一定次数后就会变成NaN或者Infinity
顺便问一下，我上面的计算步骤是有什么问题么，要做的功能就是相机跟随，上面是计算的距离跟随，角度先不管

#10

这个算法，我看了下，确实会在一定步骤之后变成 Infinity 再变成 NaN。复现代码如下：

const target = new Vec3();
const camera = new Vec3(0, 100, 0);
const minDistance = 10;
const b = new Vec3();
for (let i = 0; i < 100; ++i) {
    const deltaTime = 0.1;
    Vec3.subtract(b,  target, camera); #1
    const adj = (Vec3.len(b) / minDistance) - 1;
    Vec3.scaleAndAdd(b, camera, b, adj);
    Vec3.slerp(b, camera, b, deltaTime);
    Vec3.copy(camera, b);
}

先不管计算逻辑是否正确，可以纯纯分析下怎么就一步步变成了 NaN。记摄像机和目标的距离为 d。

  1. 第一次计算

第一次计算时，只要 d > 2 * minDistance，也就是超过了最小距离的两倍，得到的“距离比例”就会是大于 1的，也就是说在这一步计算时，理想的摄像机和目标的距离会变得更大。在给出的代码里，摄像机距离会从 100 变为原来的 100/10-1=9 倍，导致理想位置与原始位置反向。

此时得到的结果大概为这样：

image
image851×506 3.26 KB

现在进行插值，因为用的是 slerp 插值，又由于原始位置和理想位置完全反向，原始位置将 绕任意轴旋转至理想位置，若插值百分比为 0.1，则有可能得到的结果如下：

image
image850×526 4.91 KB

可以看到，发生了两个变化：

  1. 摄像机旋转了 18°（旋转了 0.1 的180°）
  2. 摄像机 更远了，因为 slerp 过程中，向量长度和方向都会向目标插值。
  1. 后面计算

从 1 可以推理出，d（摄像机和目标的距离）在不断变远，因此导致摄像机的位置越来越大以至于最后到了无穷大，又因为无穷大参与了计算导致 NaN。

为什么 lerp 没问题？

因为 lerp 和 slerp 的算法差异。对于上述的第一次计算，lerp 插值之后的结果可能如下：

image
image828×498 6.46 KB

#11

你可以试试 Math.min((minDistance / Vec3.len(b)), 1) 来作为你的“距离比例”是否合适。