在做一个生成连接线的小游戏。效果图如下：
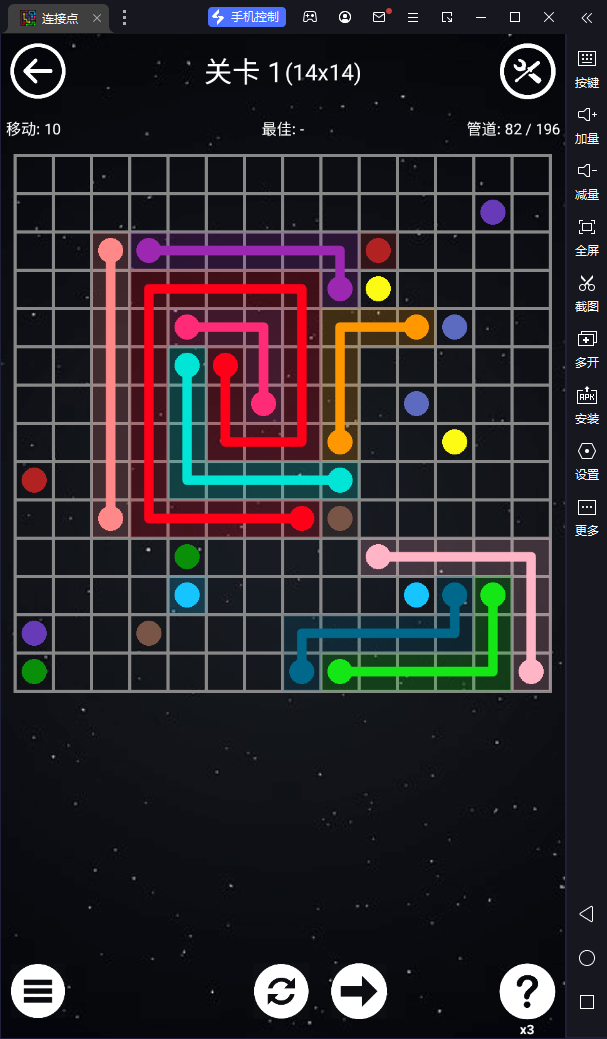
现在是要代码逻辑生成关卡数据：
目前开发逻辑：
1.在棋盘上生成随机点，点的两端自己寻找符合的下一个格子。
2.后面就回退黑块附近的端点，重新找下一个格子。
遇到的问题是：太盲目了，费时还会存在黑块，想问问大家有没有别的方法实现这个效果。欢迎讨论~
下面是手动调整的，我希望有更好的代码逻辑实现。
每个字都认识
哈哈，我个人觉得是拆分成小区域，比如说随机生成了一个行2列3的块，有3个路径可能，从中在随机找出一条，以此类推。核心思路就是拆成小块，最后找补
搜索，或者贪婪，都可以。固定数组大小的话，深度优先就可以了。
搜索相对较慢，建议先搜索生成很多结果，预存下来，然后运行的时候随机取一个。
这种类型的游戏，但要随机生成关卡
最简单就是随机生成两点，然后寻路看看能否通过，不通过时换终点，再不通过换起点，如此重复，每条生成路径把可以随机选择的格子移除 
感觉上是个 NP完全问题。(类似 四色定理)
这种问题只能暴力穷举了，然后再验证结果是否可行。
这样有可能最后剩下的格子不连续吧 
不过不具体要求必须生成多少条路径这么做是可以的。
重新整理了一下，麻烦再看看 
1. 随机关卡法
初始地图包含完整随机关卡，判断是否有解，无解重新生成。
我的猜测是，算法求解的是颜色连接的顺序。只要按照正确的顺序连接，并且每一步都采用最短路径，必定能找到解。
连接的过程本身就是最普通的寻路，采用 A* 即可。
算法过程就是暴力穷举颜色的排序。
优化点：
- 距离越短、越靠近中心，优先连接。可以先用权重对颜色做个排序。
- 缓存所有 无法联通 的颜色序列，一旦排序包含任一无法联通的序列直接跳过。
2. 逐步生成法
初始地图为空，每步随机往地图上选取两个空白点。这种情况下每一步只需要进行一次寻路即可。如果无解则重新选取两个点。直到地图填充率达到要求。
3. 迷宫生成算法
1 和 2 结合，在 1 的基础上，无路可走时删除阻碍的颜色，随机加入新的颜色
看左边绿色那里, 像这样行不行? 行的话就可以电脑直接解决掉黑色部分了啊
哈密尔顿回路问题，以前我们讨论没结果，老板直接让策划去手动配不就完了，后来做了一些辅助优化，随即撒些点什么的，连出一些最大能连的，剩下的点让策划去手动上色
不太像，这里起点是可以有任意多个的
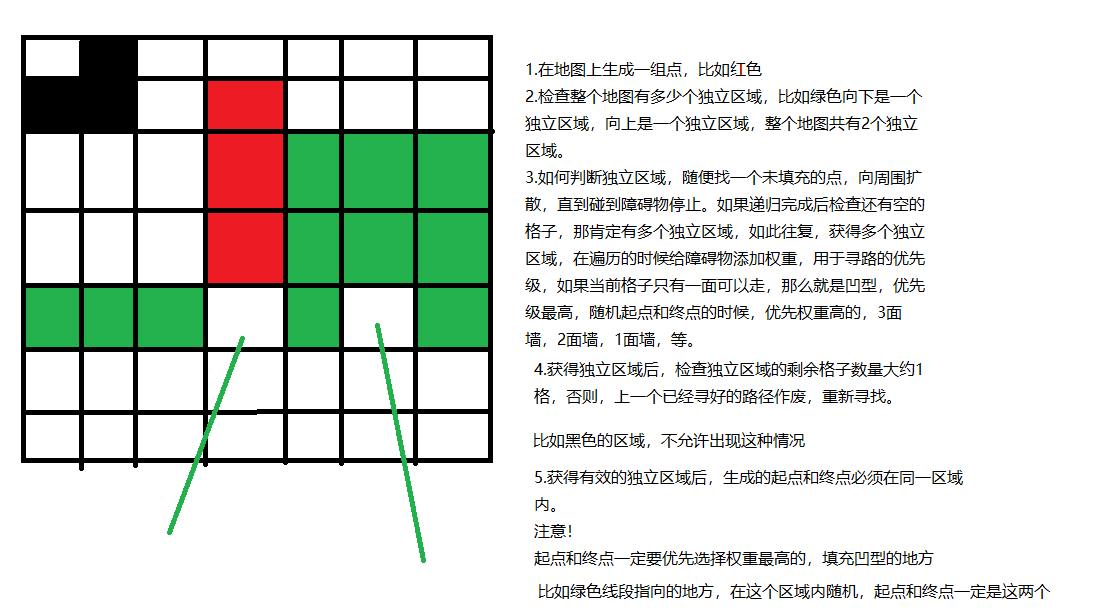
如果出现了像紫色那种特殊情况，特殊处理应该是可以解决的，理论上应该很难出现
1赞
你们讨论了半天，看上去都有点道理，但是看起来都比较复杂。还是我的深度优先搜索（你就当穷举吧），再加上预存结果比较好。
8 * 11的格子，写个代码穷举在现在的计算机上跑十来分钟估计就穷举完了。然后假设16种颜色，一个结果大概也就 11 * 8 * 4bits 存上44个字节吧。我们保底存个2000结果，也就88k的文件。
运行的时候从2000个里面随机选一个不就完了？
直接用A星寻路就好了，用A星去定好路线这些，做好关卡，这不就解决了吗