个人之前做过原型，原理上是可以的。
和React.Native比较类似，需要实现：
问题出在哪里：
所以个人结论是落地有些困难，单纯实现是没问题的。
是个不错的点子，希望能够整理为插件上架 Cocos Store
是个不错的点子，希望能够整理为插件上架 Cocos Store
点子不错。但是先做其他优先级更高的把。性能就能把这个卡的死死的
我倒是想搞个实现了，可最后使用的时候不是最好还是在 cocos 的项目里面吗，在 cocos 项目下要怎么开 jsx tsx 这些选项呢？
这块我不是很熟。直接改项目里的tsconfig.json不行吗？
compilerOptions下面加"jsx": "react",
因为 tsconfig 没有开放这些选项，加上 “jsx”: “react” 后在编辑器里面还是会报错的
如果直接写在 ts 文件里面
单独放在 tsx 文件之后
加上 “allowImportingTsExtensions”: true 之后
只有编辑器里没什么问题，不过跑不起来也没用
这也是不是就可以用cocos写小程序了。
是用类 react 的方式写 cocos
原本 cocos 在哪里还是只能在那里用
up，这个是要先学react相关然后再学cocos相关，然后才能用吗？感觉这样做游戏更麻烦了
这就不是做游戏一般做那种应用内嵌套很多游戏的社交应用
这个只是技术验证，并不是可以拿来做游戏的东西，将来应该也不太能直接拿来做游戏。
哈哈哈，邪修 
让 ai 给我解释一下这个系统，结果 o3 给我来了这么一大坨 
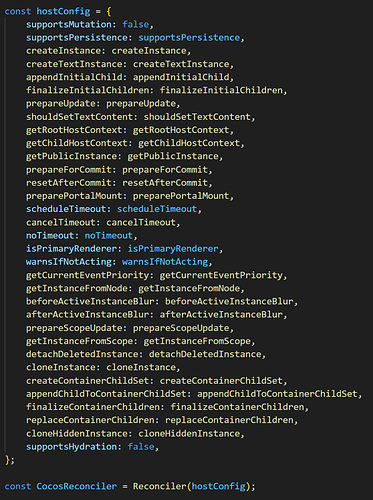
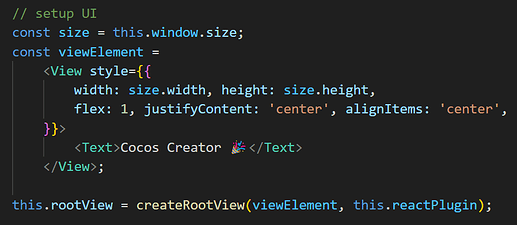
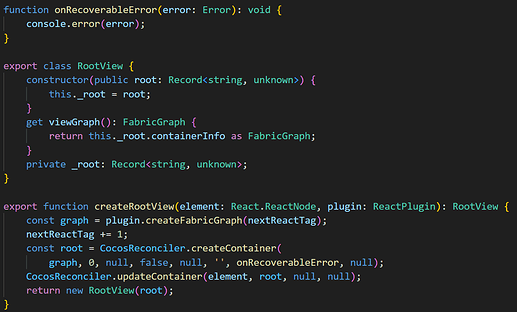
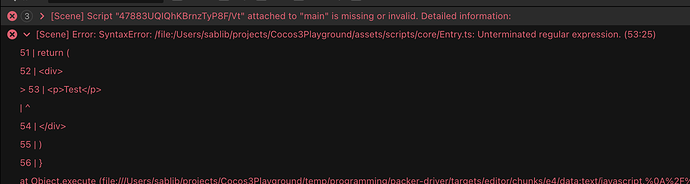
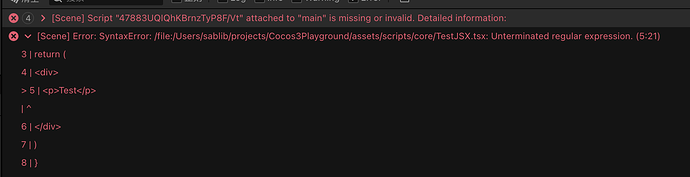
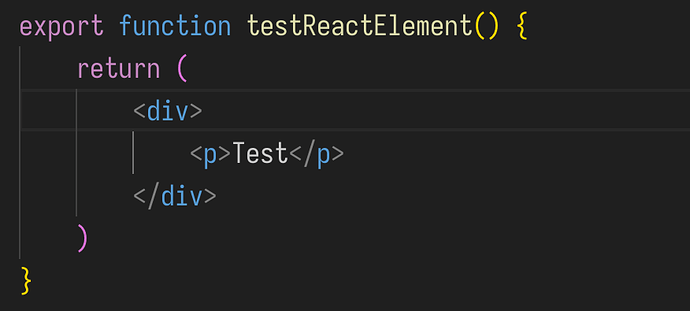
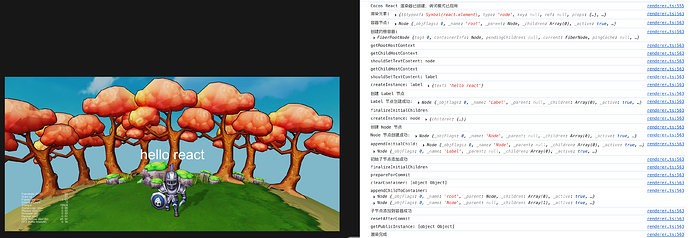
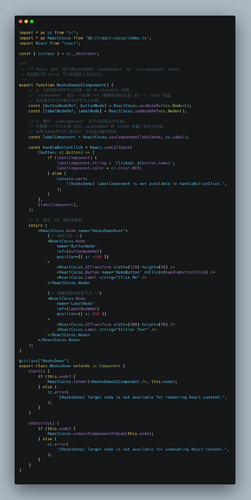
下面用较严格的「离散数学语言」重新刻画 TypeHandler Pipeline（THP）及其在
cc-node / cc-components / cc-graphics 上的具体映射，力求抽象而精确。
一、符号约定
- 记
T = {τ₁, τ₂, …} — 所有 JSX 标签类型集合
P = 属性空间 = Map〈string, any〉
N = 所有已存在的 cc.Node 实例集合
- Facet 类型族
F_Node — NodeFacet
F_Comp — ComponentFacet
F_Cont — ContainerFacet
F = F_Node ⊔ F_Comp ⊔ F_Cont ⊔ …（直和）
- 事件集合
E = {attach, applyProps, appendChild, insertBefore, removeChild, finalize}
二、Handler 与 Facet 的形式定义
- Handler
对每个 h ∈ H，给出二元组
h = ⟨testₕ, genₕ⟩
testₕ : T → {0, 1}
genₕ : T × P × (N ∪ {⊥}) → 𝒫(F) (𝒫 为幂集算子)
- Pipeline 函数
Pipeline Π : T × P × (N ∪ {⊥}) → 𝒫(F)
具体为
Π(τ, p, n) = ⋃{h∈H, testₕ(τ)=1} genₕ(τ, p, n) (1)
- MultiFacetDescriptor
D = ⟨τ, p, F_set⟩，其中 F_set = Π(τ, p, n₀)，n₀ 表示在
createInstance 时父节点未知，用 ⊥ 占位。
- 事件广播
∀f ∈ F_set, ∀e ∈ E，有映射
λ : F × E → Proc ，若 f 实现了事件 e，则 λ(f,e) = 对应过程；
否则 λ(f,e) = no-op。
HostConfig 对同一事件按注册顺序依次调用 λ(f,e)。
三、范畴化视角（简述）
• 设 ℂ 为以 Facet 为对象、事件 e∈E 为可部分定义态射的范畴。
- Pipeline Π 可视为函子
Π : (Set_Tags) → ℂ̂ (ℂ̂ 为 ℂ 的幂范畴)
——即把标签 τ 映射为 Facet 的族。
- 由于 Π 只是并集运算，天然满足函子所要求的恒等与复合保持。
（扩展一个新的 Handler 等价于向函子返回值并入一个新的对象族）
四、示例映射
- cc-node
test_node(τ) = [τ = ‘cc-node’]
gen_node(τ,p,⊥) = { NodeFacet§ }
NodeFacet 只响应 attach, applyProps。
- cc-components
test_ccc(τ)= [τ = ‘cc-components’]
gen_ccc(…) = { ContainerFacet_ccc }
其中 ContainerFacet_ccc 内部规则：
appendChild(f_child)
若 ∃ f_child ∈ F_Comp → 调用其 attach 若 ∃ f_child ∈ F_Node → parentNode.addChild(f_child.node).
- cc-graphics（双 Handler）
a) ComponentHandler_graphics
- 生成 ComponentFacet_graphics (负责安装 cc.Graphics)
b) GraphicsContainerHandler
- 生成 ContainerFacet_gfxCmd (记录 moveTo/lineTo)
根据式 (1)
Π(‘cc-graphics’, p, n) = {ComponentFacet_graphics, ContainerFacet_gfxCmd}
事件序列（简化）
text
Apply to VIRTUAL_CONT…
attach 顺序 : ComponentFacet → ContainerFacet
appendChild 顺序 : ContainerFacet 处理
finalize 顺序 : ContainerFacet 调用 graphics.stroke()
五、性质与推论
- 交换律（弱）
若两个 Facet 针对同一事件 e 互不访问共享资源，则调用顺序可交换，
即 λ(f₁,e) ∘ λ(f₂,e) = λ(f₂,e) ∘ λ(f₁,e)。
- 可扩展性
新 Handler hₙ 加入 H，只影响式 (1) 的并集，多项式时间；
HostConfig 与旧 Handler 零改动。
- 可裁剪性
若移除任意 Handler 子集 H’，得到新集合 H\H’，
Π’(τ)=Π(τ)∖⋃{h∈H’} genₕ(τ)，系统仍闭合。
六、总结
• 整套机制可视为对「标签 τ」作 多重特征分解：
Π = ⨁ testₕ·genₕ (⨁ 为特征选择后的并集算子)
- cc-node / cc-components / cc-graphics 分别通过
{NodeFacet}、{ContainerFacet}、{ComponentFacet ⊕ ContainerFacet}
实现节点、批量挂载与命令解释三种功能。
- 因为核心只实现「并集 + 广播」两步，故 任何功能扩展
都等价于在 H 里新加一条 (test, gen)。
这正是“可插拔、零耦合” 的数学本质。
