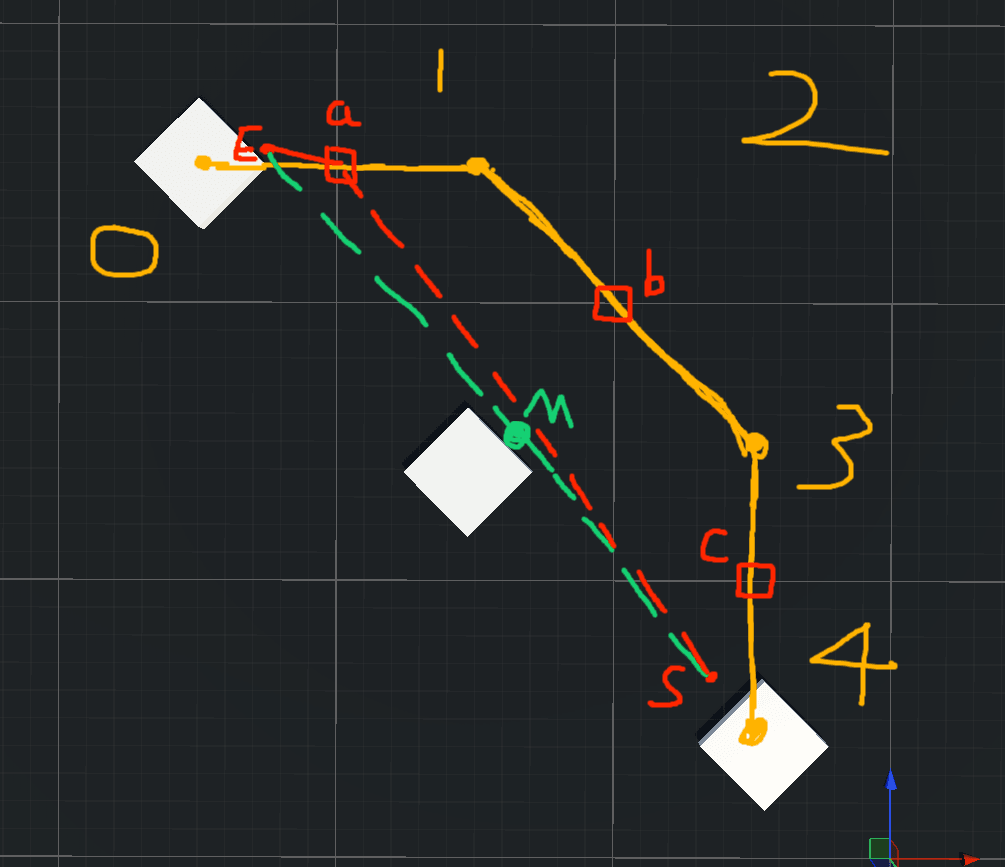
我尽量简短点
我想在原地图30 * 30也就是900格进行寻路
将原地图缩放了100倍得到了3 * 3的9格地图
因为这个地图在服务器上是二维坐标,所以只能走格子的中间点
现在开始 拼好路:起点是E,终点是S,起点位于缩放地图的0,终点位于缩放地图的4
首先在缩放的地图上找到路径:0 - 1 - 3 - 4(黄色实线)然后连接这些路径找到撞线的点,也就是红色方块
然后再分别对起点的0区域和终点的4区域进行2次精确寻路:S-边界的红色方块,E - 边界的红色方块
最终拼好路得到最终路径:E - a - b - c -S
然后我的后处理会将多余的点或者没用的点删去
最后返回:E - a -S(红色虚线) 是这个分层寻路的最终路径
实际如果使用真实寻路不使用分层寻路,那么路径是:E - M - S (绿色虚线)
我的问题是这样做的话 是不是某些情况下 偏差会特别大 比如起点E在0区域的左下角的情况,实际黄色实线可能还有N种相同的路径,比如这里的左下半部分其实也算,这样的话最终还要将所有路径拿出来比对找返回最短的那条,做出来逻辑感觉有点复杂了
这个例子障碍物不够准确 待会我更新一个