按照之前OpenGL 矩阵的理解 视图矩阵的前向量 应该是 (m08,m09,m10), 但Cocos构造的视图矩阵却是(m02,m06,m10)。如何理解?
一个列排序一个横排序本质没区别,下标不一样而已
Cocos是列主序,和 OpenGL的列主序一样,但取的相机的视图矩阵的前向量 取的却不一样,所以好奇。
z轴是第三行没问题啊
/**
* @en
* Calculates the matrix with the view point information, given by eye position, target center and the up vector.
* Note that center to eye vector can't be zero or parallel to the up vector
* @zh
* 计算视图矩阵,给定眼睛位置、目标中心和上向量。注意,中心到眼睛向量不能为零或与上向量平行。
* @out The receiving matrix.
* @param eye The source point.
* @param center The target point.
* @param up The vector describing the up direction.
* @return The receiving matrix.
*/
public static lookAt<Out extends IMat4Like, VecLike extends IVec3Like> (out: Out, eye: VecLike, center: VecLike, up: VecLike): Out {
const eyex = eye.x;
const eyey = eye.y;
const eyez = eye.z;
const upx = up.x;
const upy = up.y;
const upz = up.z;
const centerx = center.x;
const centery = center.y;
const centerz = center.z;
let z0 = eyex - centerx;
let z1 = eyey - centery;
let z2 = eyez - centerz;
let len = 1 / sqrt(z0 * z0 + z1 * z1 + z2 * z2);
z0 *= len;
z1 *= len;
z2 *= len;
let x0 = upy * z2 - upz * z1;
let x1 = upz * z0 - upx * z2;
let x2 = upx * z1 - upy * z0;
len = 1 / sqrt(x0 * x0 + x1 * x1 + x2 * x2);
x0 *= len;
x1 *= len;
x2 *= len;
const y0 = z1 * x2 - z2 * x1;
const y1 = z2 * x0 - z0 * x2;
const y2 = z0 * x1 - z1 * x0;
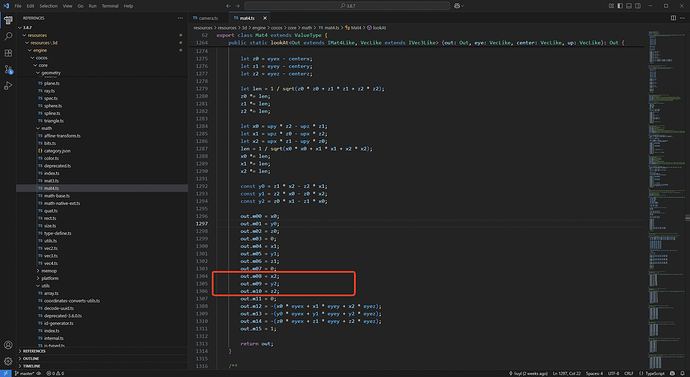
out.m00 = x0;
out.m01 = y0;
out.m02 = z0;
out.m03 = 0;
out.m04 = x1;
out.m05 = y1;
out.m06 = z1;
out.m07 = 0;
out.m08 = x2;
out.m09 = y2;
out.m10 = z2;
out.m11 = 0;
out.m12 = -(x0 * eyex + x1 * eyey + x2 * eyez);
out.m13 = -(y0 * eyex + y1 * eyey + y2 * eyez);
out.m14 = -(z0 * eyex + z1 * eyey + z2 * eyez);
out.m15 = 1;
return out;
}
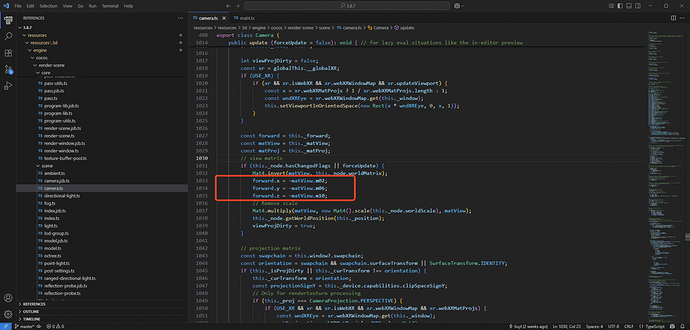
Z轴 向量 (z0, z1, z2)。 按照列主序,他应该放在m08, m09, m10,但看lookAt的实现却放在了 m02, m06, m10。 觉得奇怪。
变换到视图空间要乘以相机矩阵的逆矩阵,左上角是正交矩阵相当于乘以它的转置所以位置没问题
主要看lookAt实现,4x4视图矩阵A 的 左上角3x3矩阵B 确是正交矩阵,但只是A的部分, 而 m12,m13,m14, m15依然是第4列没有转置,还能部分转置?
按照以上结论:
| m00 m04 m08 |
| m01 m05 m09 | 正交矩阵
| m02 m06 m10 |
构造的视图矩阵
| m00 m04 m08 m12 |
| m01 m05 m09 m13 |
| m02 m06 m10 m14 |
| m03 m07 m11 m15 |
等于 它的部分转置
| m00 m01 m02 m12 |
| m04 m05 m06 m13 |
| m08 m09 m10 m14 |
| m03 m07 m11 m15 |
但真实情况不相等。
位移矩阵逆矩阵就是符号取反,代码没错的,只是你还没有完全理解变换
嗯嗯。那对于列主序的一维数组存储的矩阵
| m00 m04 m08 m12 |
| m01 m05 m09 m13 |
| m02 m06 m10 m14 |
| m03 m07 m11 m15 |
构成的矩阵空间 一般认为 (m08,m09,m10) 表示前向量,这个没有问题吧?
上面lookAt实现,却把前向量放在(m02, m06,m10),按照结果来说是没有问题,但他这么做的理由是什么。 是为了使用相机矩阵的逆矩阵?
对的,相机世界矩阵求逆其实就是观察矩阵也就是你说的视图矩阵所以这样放是对的