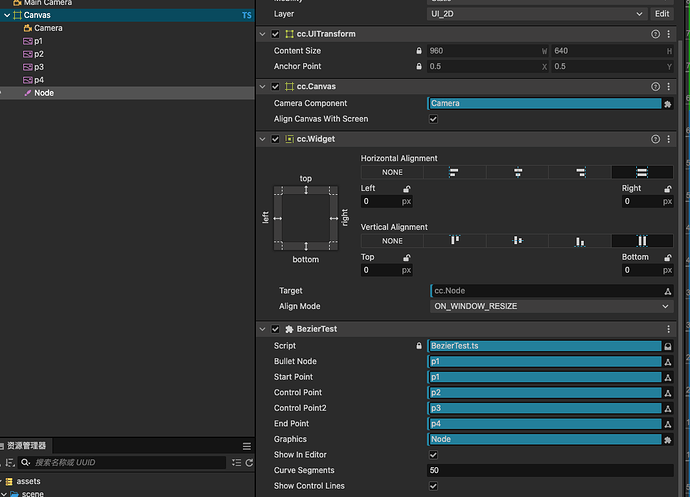
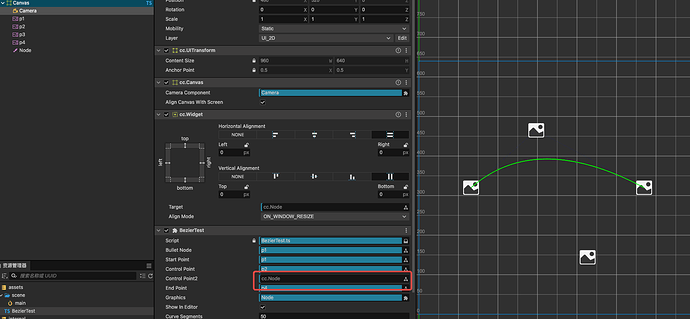
实现更加灵动的移动效果而学习的贝塞尔曲线,在此记录一下。
贝塞尔曲线一阶相当于直线了,常用的有二阶、三阶:
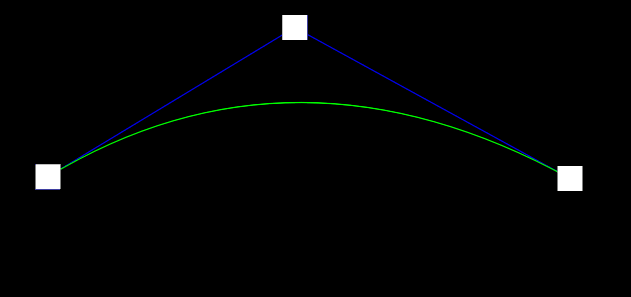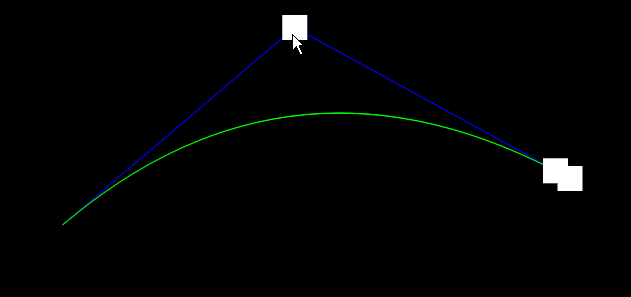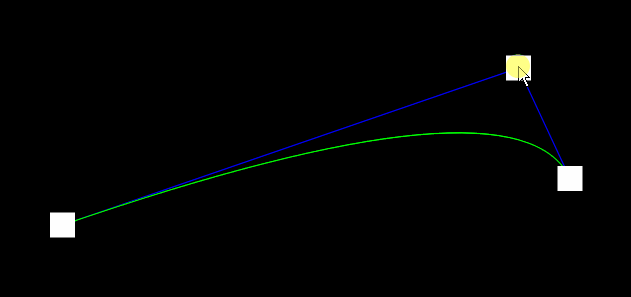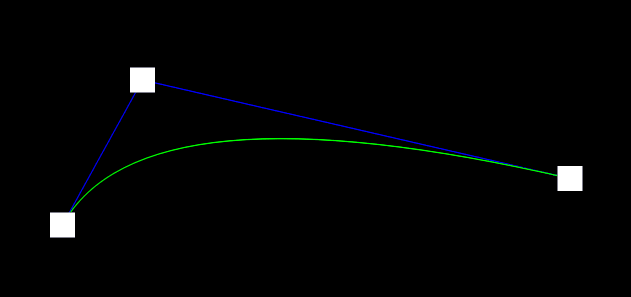
二阶曲线:
B(t) = (1-t)²P₀ + 2t(1-t)P₁ + t²P₂
基础的弧线,通过一个控制点来操控曲线的形状,主要参数有:
-
t,表示运动的进度只能取[0, 1] -
P0,表示位置的起始点 -
P1,表示弧线的控制点 -
P2,表示位置的结束点
private Bezier_Quadratic(t: number, p0: Vec3, p1: Vec3, p2: Vec3): Vec3 {
// 确保t在[0,1]范围内
t = Math.min(Math.max(t, 0), 1);
// 原式:B(t) = (1-t)²P₀ + 2t(1-t)P₁ + t²P₂
// 使用中间变量避免重复计算,令u=1-t:B(t) = uu * P₀ + _2tu * P₁ + tt * P₂
const u = 1 - t;
const uu = u * u;
const tt = t * t;
const _2tu = 2 * t * u;
// 计算x, y, z坐标
const x = uu * p0.x + _2tu * p1.x + tt * p2.x;
const y = uu * p0.y + _2tu * p1.y + tt * p2.y;
const z = uu * p0.z + _2tu * p1.z + tt * p2.z;
return new Vec3(x, y, z);
}
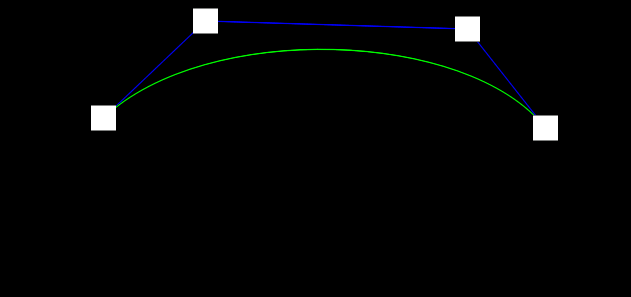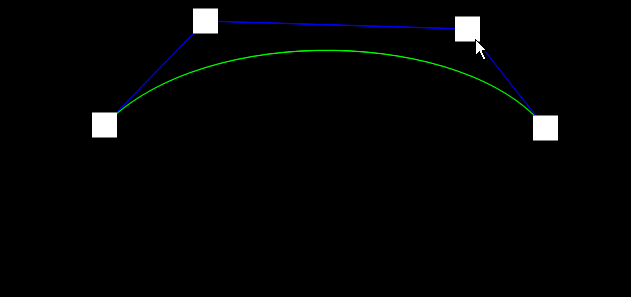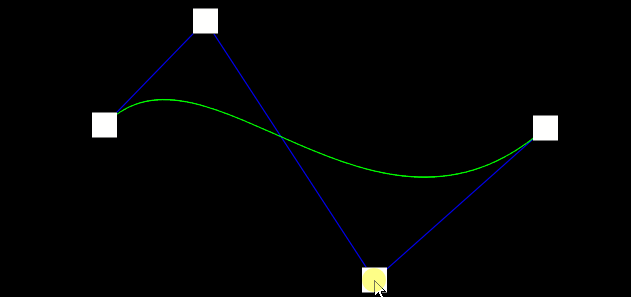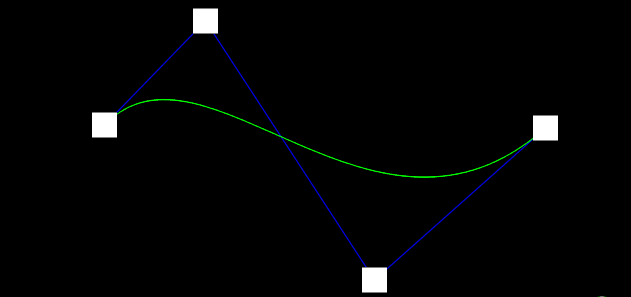
三阶曲线:
B(t) = (1-t)³P₀ + 3t(1-t)²P₁ + 3t²(1-t)P₂ + t³P₃
通过两个控制点来操控曲线的形状,可以描绘更复杂的曲线 & 更平滑的过渡,主要参数有:
-
t,表示运动的进度只能取[0, 1] -
P0,表示位置的起始点 -
P1,表示弧线的控制点1 -
P2,表示位置的控制点2 -
P3,表示位置的结束点
private Bezier_Cubic(t: number, p0: Vec3, p1: Vec3, p2: Vec3, p3: Vec3): Vec3 {
// 确保t在[0,1]范围内
t = Math.min(Math.max(t, 0), 1);
// 原式:B(t) = (1-t)³P₀ + 3t(1-t)²P₁ + 3t²(1-t)P₂ + t³P₃
// 使用中间变量避免重复计算,令u=1-t:B(t) = uuu * P₀ + _3tuu * P₁ + _3ttu * P₂ + ttt * P₃
const u = 1 - t;
const uu = u * u;
const uuu = uu * u;
const tt = t * t;
const ttt = tt * t;
const _3tuu = 3 * t * uu;
const _3ttu = 3 * tt * u;
const x = uuu * p0.x + _3tuu * p1.x + _3ttu * p2.x + ttt * p3.x;
const y = uuu * p0.y + _3tuu * p1.y + _3ttu * p2.y + ttt * p3.y;
const z = uuu * p0.z + _3tuu * p1.z + _3ttu * p2.z + ttt * p3.z;
return new Vec3(x, y, z);
}
练习案例
以二次贝塞尔曲为例,模拟子弹发射,那么要解决的有两个问题:
- 子弹怎么沿曲线移动
- 子弹在移动过程中的角度问题
角度问题
子弹沿曲线前进,需要让子弹的朝向与运动方向一致。
我使用的是 计算二次贝塞尔曲线在 t 时刻的切线方向,即对B(t)求导。
然后再根据切线得到角度。
private calculateQuadraticBezierTangent(t: number, p0: Vec3, p1: Vec3, p2: Vec3): Vec3 {
// 二次贝塞尔曲线
// 原式:B(t) = (1-t)²P₀ + 2t(1-t)P₁ + t²P₂
// 求导:B'(t) = 2(1-t)(P₁-P₀) + 2t(P₂-P₁)
const u = 1 - t;
const dx = 2 * u * (p1.x - p0.x) + 2 * t * (p2.x - p1.x);
const dy = 2 * u * (p1.y - p0.y) + 2 * t * (p2.y - p1.y);
return new Vec3(dx, dy, 0).normalize();
}
沿曲线移动
我用的是 tween & onUpdate 方法来实现的:
private startBezierMovement(targetNode: Node, startPos: Vec3, control1: Vec3, endPos: Vec3): void {
// 使用虚拟对象进行tween
const tweenObj = { progress: 0 };
tween(tweenObj)
.to(1, { progress: 1 }, {
onUpdate: (target: any, ratio: number) => {
const t = target.progress;
// 计算当前位置
const position = this.Bezier_Quadratic(t, startPos, control1, endPos);
targetNode.setPosition(position);
// 当前切线
const tangent = this.calculateQuadraticBezierTangent(t, startPos, control1, endPos);
// 计算角度(弧度)
const angle = Math.atan2(tangent.y, tangent.x);
// 转换为度数并设置旋转
const degrees = angle * 180 / Math.PI;
targetNode.setRotationFromEuler(0, 0, degrees);
},
onComplete: () => {
console.log('贝塞尔曲线运动完成');
}
})
.start();
}
随机控制点
再对控制点加上一点随机,我这里用的是起始、结束两点间中垂线上随机距离:
// 计算中点
const midPoint = startPos.clone().lerp(endPos, 0.5);
// 计算方向向量(从起点到终点)
const direction = endPos.clone().subtract(startPos).normalize();
// 计算垂直向量(垂直于连接线)
const perpendicular = new Vec3(-direction.y, direction.x, 0).normalize();
// 在垂直方向上随机偏移(实际上我们只需要上下方向,所以用(0,1,0)或者计算出的垂直向量)
const randomHeight = Math.random() * 1200 - 600;
// 控制点位于中点正上方(或正下方)的垂直线上
const control1 = midPoint.clone().add(new Vec3(0, randomHeight, 0));
效果

去掉辅助线,再随机起始时间后的效果:

顺带一提
辅助线的绘制:
/** 绘制贝塞尔曲线路径 */
private drawBezierPath(p0: Vec3, p1: Vec3, p2: Vec3, p3?: Vec3) {
const graphics = this.graphics;
graphics.moveTo(p0.x, p0.y);
if (p3) {
graphics.bezierCurveTo(p1.x, p1.y, p2.x, p2.y, p3.x, p3.y);
} else {
graphics.quadraticCurveTo (p1.x, p1.y, p2.x, p2.y);
}
graphics.stroke();
}