谁能告诉我误差的计算，为什么是拿传的误差的值去乘以x,y,z的绝对值的最大值 来当范围比较
只有这个是我理想的结果
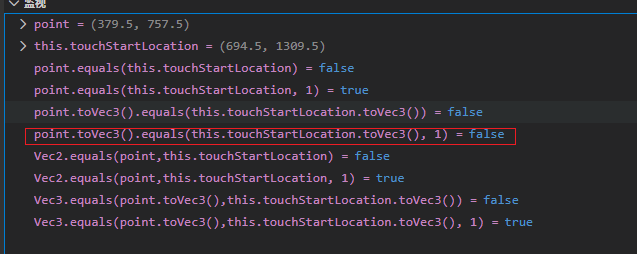
问AI吧 这种设计是一个 相对误差与绝对误差结合 的混合比较方法，比简单的绝对误差比较更健壮。让我们分解一下：
1. 核心公式
typescript
abs(a - b) <= epsilon * max(1.0, abs(a), abs(b))
2. 为什么要这样设计？
情况1：小数值范围（接近0）
当 |a| 和 |b| 都小于1时：
max(1.0, abs(a), abs(b)) = 1.0- 公式简化为：
abs(a - b) <= epsilon - 这是绝对误差比较 ，确保接近0的值也能被正确比较
情况2：大数值范围
当 |a| 或 |b| 大于1时：
-
max(1.0, abs(a), abs(b))取较大的那个值 - 公式变为：
abs(a - b) <= epsilon * max_value - 这是相对误差比较 ，误差容忍度随数值大小成比例变化
3. 与简单比较的对比
简单绝对误差（有问题）：
typescript
abs(a - b) <= epsilon
- 问题：对于大数值（如10000.0和10000.1），0.1的差异可能不重要，但会判为不等
- 问题：对于小数值（如0.00001和0.00002），0.00001的差异相对很大，但会判为相等
简单相对误差（也有问题）：
typescript
abs(a - b) <= epsilon * abs(a)
- 问题：当
a ≈ 0时，误差容忍度趋近0，过于严格 - 问题：不对称（依赖a而不是b）
4. 实际例子
typescript
const EPSILON = 1e-6; // 例子1：小数值 equals(0.000001, 0.000002, 1e-6) // abs(0.000001) <= 1e-6 * max(1.0, 0.000001, 0.000002) // 0.000001 <= 1e-6 * 1.0 = 1e-6 
相等（绝对误差主导） // 例子2：大数值 equals(10000.0, 10000.01, 1e-6) // abs(0.01) <= 1e-6 * max(1.0, 10000.0, 10000.01) // 0.01 <= 1e-6 * 10000.01 ≈ 0.01 相等（相对误差主导） // 例子3：中等数值 equals(1.0, 1.000001, 1e-6) // abs(0.000001) <= 1e-6 * max(1.0, 1.0, 1.000001) // 0.000001 <= 1e-6 * 1.000001 ≈ 1e-6 相等
5. 设计优点
- 数值稳定性 ：处理各种数量级的数值
- 对称性 ：不依赖哪个值作为参考
- 边界友好 ：特别处理接近0的情况
- 物理意义 ：既考虑绝对精度也考虑相对精度
6. 典型应用场景
- 图形计算（3D变换、插值）
- 物理模拟（位置、速度比较）
- 游戏开发（碰撞检测、坐标比较）
- 数值优化（收敛判断）
这种设计在计算机图形学和数值计算中很常见，是处理浮点数比较的行业标准做法之一。
主要问题还是，Vec3那边有相对误差+绝对误差两种，但是Vec2那边误差只有相对误差一种，应该Vec2那边也保留一个绝对值误差
我之前用Vec3身上的equals没问题，然后用Vec2的equals一直感觉不对劲，一看代码才发现写的不一样。。。