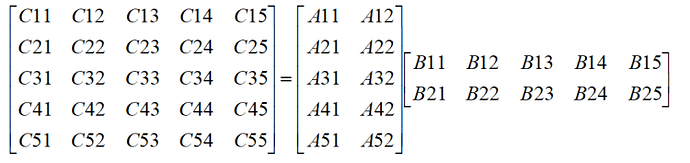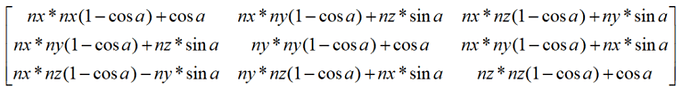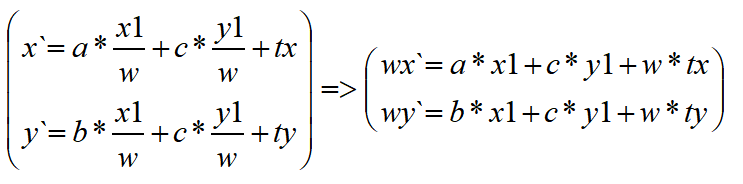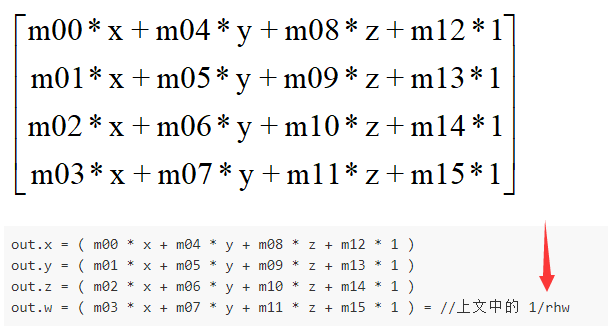导读:
-
了解分析Cocos其中的一个坐标变换方法convertToWorldSpaceAR的实现
-
通过上述方法的实现了解矩阵相关知识
-
了解常见的几种矩阵变换,旋转、缩放、平移等
-
了解齐次坐标
首先,我们在Cocos开发当中经常会用到Node的方法convertToWorldSpaceAR(3.x以上版本在UITransform类里面)变换某个坐标到世界坐标空间下或者使用convertToNodeSpaceAR方法变换某个世界坐标到当前节点空间坐标系下。
我们是否有了解过对应方法是如何实现的呢?下面我们直接来看一看相关接口源码(3.x版本)
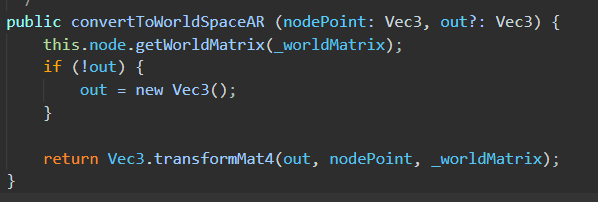
(源码路径:resources\resources\3d\engine\cocos\2d\framework\ui-transform.ts)
简单描述一下方法的实现:就是获取当前节点的世界矩阵,然后使用
Vec3.transformMat4方法把传入的节点坐标nodePoint变换到世界空间下的坐标点。
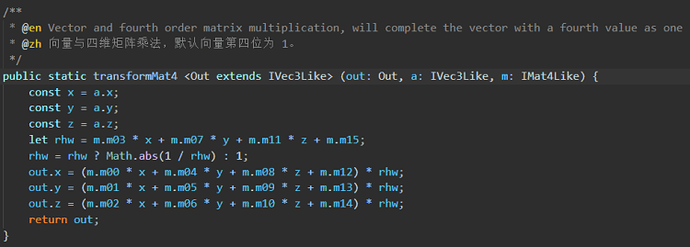
那么我们再看看Vec3.transformMat4方法具体做了什么吧。
(源码路径:\resources\resources\3d\engine\cocos\core\math\vec3.ts)
如果在不了解矩阵的情况下,可能看到这些计算会一头雾水,不知道它具体怎么实现的。
因此我们必须先了解矩阵相关定义,从而了解矩阵如何变换坐标的。
矩阵
(PS:更多详细的关于矩阵的知识可以参考相关线性代数书籍)
1.一个nxm的矩阵表示由n行m列的数字组成的行列式。
例如:4x4的矩阵M表示如下
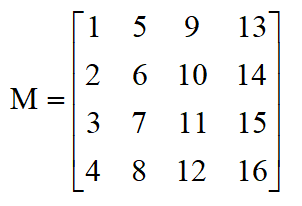
2.如果矩阵M的行与列数相同时,可以称矩阵M为方阵。
例如我们游戏中经常用到的用于变换的方阵就有3x3方阵,4x4方阵。
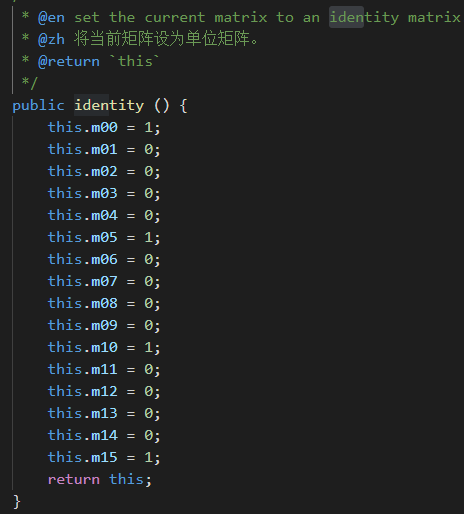
3.单位矩阵:当正对角线的值都为1,且其他位置的值都为0的方阵称为单位矩阵
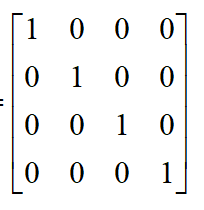
4.矩阵相乘:矩阵A与矩阵B相乘,当且仅当矩阵A的列与矩阵B的行数量相同时才能相乘。
例如A为5x2矩阵 B为2x5矩阵。他们相乘的结果AB为5x5的矩阵C。
C的第i行第j列的值=A的第i行与B的第j列的点积
那么C的第2行第4列的元素就是等于A的第2行和B的第4列的点积。
C24 = A21 * B14+A22 * B24
5.相乘不满足交换律,但满足结合律。
AB!=BA
A(BC)=(AB)C
6.单位矩阵I与其他矩阵M相乘,矩阵不变
IM = M
那么我们经常用到的二维向量,三维向量其实也是矩阵的一种。以三维向量(1 2 3)为例。横着看可以看作1x3的矩阵,也可以称为行向量。
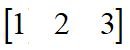
竖着写可以看作3x1的矩阵,也称为列向量。
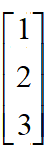
那么,对于上述方法而言,其实是做了一次矩阵相乘的操作之后得到了变换后的坐标。
那么我们是以行向量还是以列向量来计算呢?
Cocos里的存储矩阵都是按主列序的(PS:webGL跟openGL里面存储的也是按照列主序的,Cocos这里应该是为了统一方便)
以下我们说的矩阵相乘都是按列主序来讲的,向量也就是按照列向量来说。那么一个4x4的矩阵各个元素应该是按照如下排序
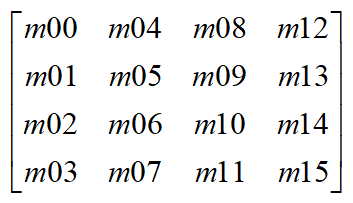
至此我们应该掌握基本的矩阵知识了。
那么我们再反回去看看transformMat4方法的逻辑,至少知道了其实是一个向量(矩阵)与矩阵相乘。
由于是3维向量,不能直接与4x4矩阵相乘,那么我们扩充3维向量到4维,向量第四位为1,来看看他们的计算结果,至于为什么要扩充呢?我们暂时带着这个疑问,先看看相乘之后的结果。
//源码
public static transformMat4(out: Out, a: IVec3Like, m: IMat4Like) {
const x = a.x;
const y = a.y;
const z = a.z;
let rhw = m.m03 * x + m.m07 * y + m.m11 * z + m.m15;
rhw = rhw ? Math.abs(1 / rhw) : 1;
out.x = (m.m00 * x + m.m04 * y + m.m08 * z + m.m12) * rhw;
out.y = (m.m01 * x + m.m05 * y + m.m09 * z + m.m13) * rhw;
out.z = (m.m02 * x + m.m06 * y + m.m10 * z + m.m14) * rhw;
return out;
}
则变换后的坐标out为

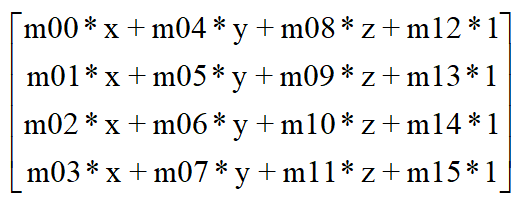
out.x = ( m00 * x + m04 * y + m08 * z + m12 * 1 )
out.y = ( m01 * x + m05 * y + m09 * z + m13 * 1 )
out.z = ( m02 * x + m06 * y + m10 * z + m14 * 1 )
out.w = ( m03 * x + m07 * y + m11 * z + m15 * 1 ) = //上文中的 rhw
可以对比一下源码,对应实际输出的坐标就是(out.x/out.w, out.y/out.w, out.z/out.w)为什么这里要除去out.w呢,这里是有关齐次坐标一些概念,后文会提到。
到此,我们了解了矩阵是怎么变换坐标的了。那为什么我们要采用矩阵来做变换呢?
首先我们常见的变换有哪几种呢?看一下节点面板就知道了。

我们经常用到的就是平移、旋转、缩放(其他的还有切变skew,投影,镜像等等),而且我们在变换过程当中往往不止是只做其中一种变换,而是多种变换一起。
采用矩阵变换的好处:那么根据矩阵的乘法规则以及结合律我们可以在得到对应平移、旋转、缩放等变换矩阵之后,根据变换先后顺序把相应的变换矩阵相乘,整合到一个整体的变换矩阵,然后再对节点坐标进行变换,仅仅使用一个矩阵就能存储下节点的所有变换,方便我们计算,减少了中间变换的一些操作。
那么下面分别对上述变换做一个简单的变换操作说明,并得出对应变换矩阵。
缩放
先由浅入深,以2D笛卡尔坐标系下的一个点A(x1,y1)进行缩放变换。缩放因子为sx,sy,分别对应着X轴缩放sx,Y轴缩放sy。缩放之后的坐标B为(x,y)。则我们可以列出等式:
x` = sx*x1
y` = sy*y1
那么如何以矩阵的形式来表示呢?
根据相乘法则我们可以知道该缩放矩阵是2x2的矩阵,则有
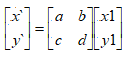
根据相乘运算展开可得
x` = a * x1+b * y1 = sx * x1
y`= c * x1+d * y1 = sy * y1
对比可以得到a=sx b=0 c=0 d=sy
则得到对应2D缩放矩阵为
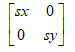
采用同样的方法,我们可以简单得出3D坐标系下,缩放因子为(sx sy sz)的缩放矩阵为
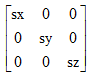
旋转
类似地
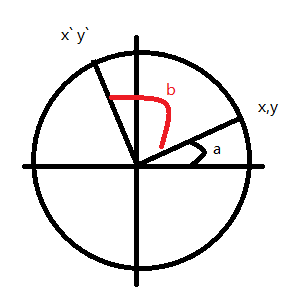
在2D坐标系下的一个单位圆上的所有坐标都可以表示成(cosa,sina),那么对应坐标系中的某一点坐标A(x1,y1)可以表示为半径为r,绕X轴逆时针旋转了a弧度的坐标。
A = (r * cosa, r * sina)
那么对于点A经过旋转b弧度后的坐标B(x,y)
B = (r * cos(a+b), r * sin(a+b))
利用三角函数展开可以得到
x1 = r*cosa y1 = r*sina
x` = r*(cos(a+b))
= r*(cosa*cosb-sina*sinb)
= r*cosa*cosb-r*sina*sinb
= x1*cosb-y1*sinb
y` = r*(sin(a+b))
= r*(sina*cosb+cosasinb)
= r*sina*cosb+r*cosa*sinb
= y1*cosb+x1*sinb
由上述可以变换得到旋转变换矩阵为
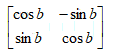
类比到3D坐标系下,我们可以分别得到绕X,Y,Z轴旋转的旋转变换矩阵。
一般地,当我们绕某一特定坐标轴旋转,那么对应该轴的坐标是不会发生变化的,相当于转化成在该轴的对应点上平行于其他两个轴的平面上做旋转。
例如 3D坐标系下,当绕X轴旋转(x,y,z)坐标的时候,X轴坐标是不变的,那么y,z坐标实际上就是在2D平面下做了旋转。
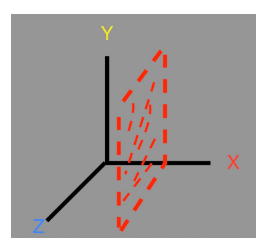
依据上述原理可以比较快得出绕X轴旋转的3D坐标系下的旋转b弧度的旋转变换矩阵。这里不再写出求解公式。
绕X轴旋转的旋转变换矩阵:
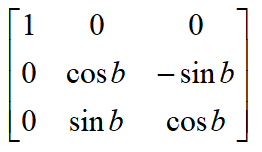
绕Y轴旋转的旋转变换矩阵:
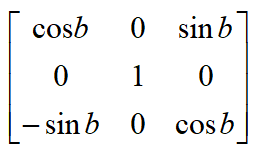
绕Z轴旋转的旋转变换矩阵:

细心的你应该会发现,怎么绕Y轴旋转的三角函数值不太一样,咋回事呢?
下面我们细说一下绕Y轴旋转的变换矩阵由来。
其实造成这个的原因是因为坐标系的相互顺序导致的。以我们用到的右手坐标系为例,各个轴之间相互顺序必须符合右手法则。也可以用叉乘来表示,例如现在轴X,Y, XxY把X的头与Y的尾相接,在右手坐标系下,XY相连,呈逆时针的则叉乘结果向量就指向屏幕前的你,否则相反。
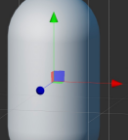
如图,Cocos内的一个坐标系,红色箭头方向为X轴正方向,绿色箭头为Y轴正方向,蓝色箭头为Z轴正方向。
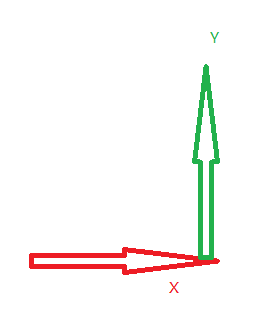
逆时针方向
那么对于Cocos的坐标系来说轴X叉乘轴Y是逆时针,结果则是:Z轴正方向指向屏幕的你,Cocos的坐标系也是采用右手系的。
那么根据右手定则循环不变性,如果XxY->Z的话,则有YxZ=X,ZxX=Y。那么当我们从Y轴往反方向看过去,形成的坐标系应该是如下图这样子的,即Z为横轴,X为纵轴,计算旋转的时候是Z-X平面
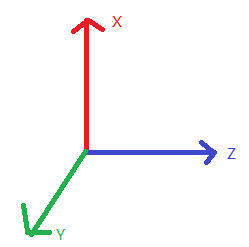
根据之前2D平面下的计算方法可以得到
z1 = r*cosa x1 = r*sina
z` = r*(cos(a+b))
= r*(cosa*cosb-sina*sinb)
= r*cosa*cosb-r*sina*sinb
= z1*cosb-x1*sinb
x` = r*(sin(a+b))
= r*(sina*cosb+cosasinb)
= r*sina*cosb+r*cosa*sinb
= x1*cosb+z1*sinb
那么就可以得出对应上面写的矩阵了。
绕任意轴旋转
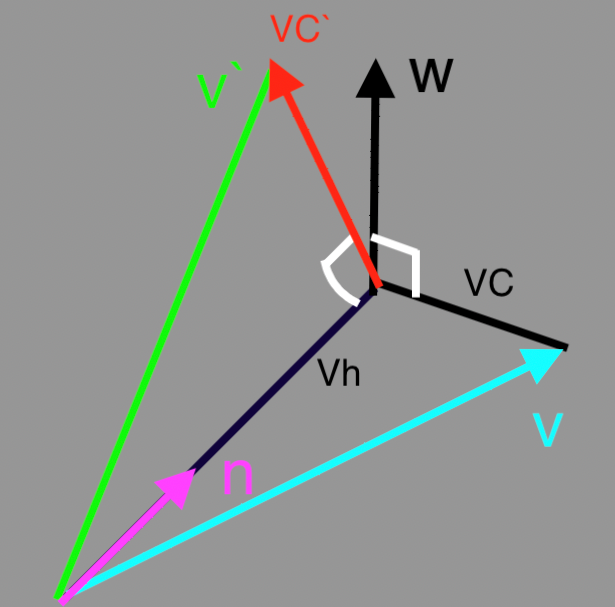
那么设定3D坐标系下任意轴的单位向量为n,假定n(nx, ny, nz)是过原点的,如果不过原点可以先平移到原点计算得到之后再平移回去,蓝色向量v绕轴n旋转a弧度得到绿色v`。旋转变换矩阵为R(n,a)
则有
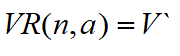
如何求得矩阵R(n,a)呢,可以根据上图分解之后的分量求证。下面简单说一下证明步骤。只要我们找到向量n、V与V`之间的相互转换关系,就可以采用上面代入方程来求解到相应的矩阵元素。
- Vh是V在向量n上的投影向量,通过点乘可以求得
- 向量V=Vh+VC
- 同理绕任意轴n旋转之后得到对应的向量就是V
VC - 向量V
= Vh+VC - VC可以由V-Vh获得
- VC
可以从VC由2D平面的旋转变换可以得到VC=VCcosa+Wsina(W是可以通过Vh叉乘VC得到) - 由此就可以用得到V`与向量n和V的相互关系。然后逆推出矩阵。详细的过程大家可以搜索一下相关教程,或者尝试自己推导一下。下面直接给出最终矩阵,有个印象。
平移
当A(x1,y1)发生平移(tx,ty)个单位,则平移后的坐标B(x,y)可以表示为
x` = x1+tx
y` = y1+ty
你会发现,对应平移等式无法推导变成2x2矩阵的线性变换。那么可以看出来平移变换不是线性变换。但可以变成如下形式的矩阵变换,先与单位矩阵相乘(可忽略)再与平移形成的矩阵相加。
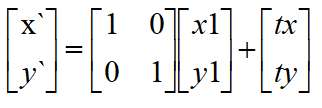
显然,上面这样子做显得有点膈应了,这跟我们的初衷不一样了,我们是想着在一个矩阵里面计算最终的变换,但平移却没有办法用矩阵相乘的形式来表示。
回过头来,还记得上面留下的疑问吗,为什么我一个3维的坐标不能直接用一个3x3的矩阵来进行变换呢?原因之一,那就是3x3矩阵对3维坐标进行变换无法表达平移变换。所以我们得加多一个维度来表示平移变换。也就是我们最后要提到的一个概念:齐次坐标。
下面给出齐次坐标一些相关的概念。
齐次坐标
1.齐次坐标其实是为了方便我们计算的一种技巧,手段。它表示将一个原本n维的向量用一个n+1维的向量表示,是指一个用于投影几何里面的坐标系统。区别于我们经常用到笛卡尔坐标系,类似的还有其他坐标系,譬如极坐标系。
2.譬如一个2D笛卡尔坐标系下的点A(x,y)的齐次坐标就形如(x,y,w)的形式存在,设定w=1时是标准的2D平面,那么实际上A点在齐次坐标下就表示为(x,y,1)
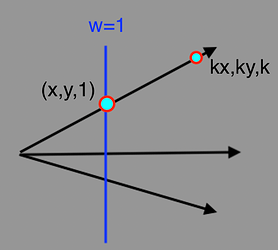
3.对于w!=1的情况下,我们把它投影到w=1的标准平面上,则2D坐标点就是(x/w,y/w) w!=0(w=0时其实描述的是一个方向或者说是一个无穷远的点。
4.那么对于给定的一个2D(x,y)坐标点,在齐次坐标空间中有无数个点与之对应(kx,ky,k) k!=0,这些点构成了穿过齐次坐标空间原点的一条直线。
回到平移变换当中来说,我们怎么比较通俗的理解呢?我们无非是想平移变换也能够采用矩阵相乘的办法来标识。
显然,在笛卡尔坐标系下增加了平移变换之后一般形式可以写成
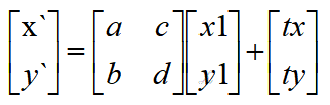
通过展开可以的到
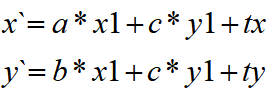
齐次坐标空间下,把对应坐标点(x1,y1)扩展为(x1,y1,w) w!=0,替换上述式子,及x1,y1变成x1/w y1/w, 通过等式乘w则变成了
由式子可以看到,在齐次坐标空间下,平移操作用矩阵乘法来表示变得有意义了。通过扩展到3维齐次坐标下也就是使用3x3的矩阵来表示。
我们现在假设w总是等于1(在标准平面上).那么标准2D坐标(x,y)对应的其次坐标为(x,y,1),那么任意的2x2的变换矩阵在3维齐次坐标空间下表示如下图(通过替换对应值很容易把2D旋转,缩放矩阵转化为齐次坐标空间下的变换矩阵)
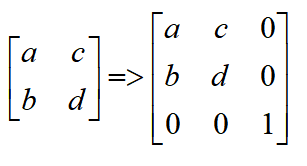
那么通过上述式子很容易得到对应平移变换矩阵则是
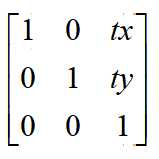
2D坐标的平移变换矩阵
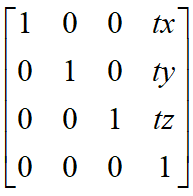
3D坐标的平移变换矩阵
到此,再看回上面提过的tramsformMat4的方法中的两个疑问就迎刃而解了。搞懂之后基本可以了解到坐标中的一些常用的变换是如何进行的。在Vec3 Vec2 Mat4等等一些类的接口用起来也会比较得心应手了。
本文如有错漏之处,欢迎指正!